Newtonian Flows

The impact theory Newton proposed, is simply to calculate the normal force on a plate at angle в in terms of the change of normal momentum, i. e. (Fig. 12.3)

N = Ap0U2 sin2 в (12.121)

hence

Cp = P – P0 = 2sin2 в (12.122)

2 P0U 2

For a curved surface, the modified Newtonian theory is

Cp = Cp, max sin2 в (12.123)

where Cp, max is the stagnation pressure coefficient. Indeed, as M0 ^ ж, the flow across a normal shock gives Cp, max = 2. However, for finite M0, Cp, max < 2. See Fig. 12.4.

On the other hand, the oblique shock relations are given by

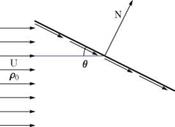
Fig. 12.3 Newton’s impact theory

Fig. 12.4 Modified Newton’s theory

since both в and в are small.

The pressure coefficient is given by

where U and R are the mean values of the velocity and of radius of curvature of the thin layer of thickness N, see Fig. 12.5.

The mass flow rate past a section of a body of revolution is given by

Ґ 2

m = 2nr pudn — nr zp0U (12.128)

0

Notice, rs — r. Hence

Fig. 12.5 Shock layer

и r r, r и

Ap = P0U2, and Cp = (12.129)

R 2 R U

As M0 and y ^ 1, a particle entering the shock with a tangential velocity

U cos в retains that velocity, therefore the mean velocity U is

1 Ґ

u= 2nrU cos edr (12.130)

nr2 0

The radius of curvature of the thin layer is governed by

r d в

= r sin в (12.131)

R dr

Hence,

sin в dв r

ACP = 2 cos вrdr (12.132)

r dr 0

Let A = nr2, the cross-sectional area; The modified surface pressure coefficient given by Busemann is

2 dв fA

Cp = 2 sin2 в + 2 sin в cos вdA (12.133)

dA J0

For a sphere, the above relation becomes

Cp = 2^1 – 4 sin2 ^ (12.134)

Lighthill [65] suggested that the shock wave separates from the surface of the sphere at the point of vanishing Cp, в = 60° measured from the forward stagnation point, Fig. 12.6.

Fig. 12.6 Sphere in Hypersonic Flow

The shape of the shock wave may be determined from

d – a

0 = 2sin2 в + 2sine – cos edA (12.135)

dA Jq

It can be shown that the shock shape tends asymtotically to be y ~ x1/3.

The modified Newton-Busemann formulas for slender bodies are

Cp = Cp0 (в2 + Г-‘J, for axisymmetric flow (12.136)

Cp = Cp0 (в2 + y-‘J, for plane flow (12.137)

For cones and wedges, the Busemann corrections vanish and the Newtonian for­mulas are consistent with the shock relations as M0 ^<x> and у ^ 1.