Profile Drag Prediction

The prediction of profile drag Dp can be performed using a number of different approaches. These are presented in the subsequent sections in order of increasing accuracy and also increasing cost and complexity.

1.12.2 Wetted-area methods

The so-called wetted-area methods are based on the drag of a zero-thickness flat plate with a constant freestream edge velocity, ue — V^. In this case there is no pressure drag, so that the profile drag consists entirely of friction drag which can be conveniently given in terms of an average skin friction coefficient Cf based on the freestream dynamic pressure qto.

Here, £ is the streamwise length of the boundary layer flow, which also defines the streamwise-length Reynolds number Beg. The wetted area Swet is defined as the surface area in contact with the moving fluid, which for the flat plate is twice the planform area. The average skin friction coefficient is obtained

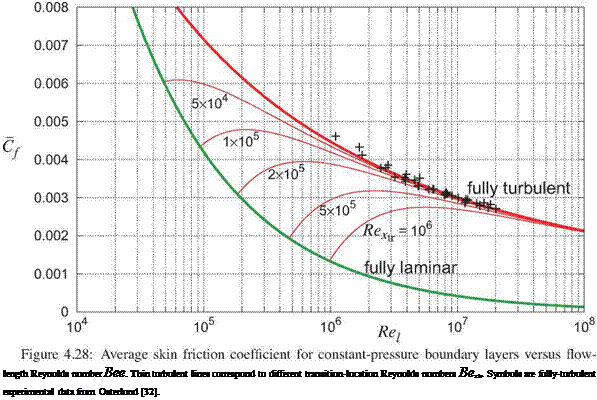These Cf functions are shown in Figure 4.28. The added transition-location term in (4.107) is based on the formulation of Schlichting [12], and depends on the transition-length Reynolds number Bextr.

For bodies other than flat plates, the profile drag is assumed to be given by

where Kf > 1 is an empirical form factor which depends on the shape of the body, and possibly also on the angle of attack and Mach number. Hoerner [33] gives extensive data for form factor values for a variety of 2D and 3D body shapes.

The main shortcoming of the wetted-area profile drag estimate (4.109) is that it’s not really predictive, but is in effect a means of experimental drag interpolation or extrapolation via the assumption that the form factor Kf does not change much over the range of body shapes being considered. If modifications in the
body shape change Kf in some unknown way which is not accounted for, then the resulting profile drag predictions for the modified body shapes will be inaccurate. In other situations where novel or unusual body shapes are being examined and drag data is not available, then the necessary Kf values must be guessed and the resulting drag estimates become uncertain.