Regimes of Compressible Flow
For steady, inviscid and adiabatic flows, Bernoulli’s law is
У 2
H = h + — = C (12.1)
where C is constant along a streamline and h = CpT for a perfect gas.
The above relation can be rewritten in terms of the speed of sound (a2 = y RT) as
y 2 + 2 a2 = const = y2ax (12.2)
Y – 1
where ymax is the maximum possible velocity in the fluid (where the absolute temperature is zero) corresponding to the escape velocity when the fluid is expanded to vacuum (Fig. 12.1).
© Springer Science+Business Media Dordrecht 2015 399
J. J. Chattot and M. M. Hafez, Theoretical and Applied Aerodynamics,
DOI 10.1007/978-94-017-9825-9_12
|
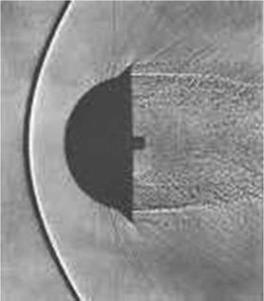
In the following sketch, the different regimes of compressible flow are identified and hence their physical characteristics are discussed, see Fig. 12.2.
(i) For incompressible flow M ^ 1, V ^ a and Aa ^ AV
Notice that
2
V AV + aAa = 0 (12.3)
7 – 1
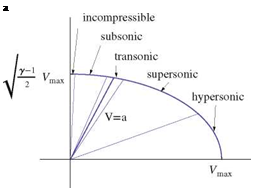 Fig. 12.2 Regimes of compressible flow
Fig. 12.2 Regimes of compressible flow
(ii) For subsonic flow M < 1, V, a and |Aa| < IA V |
(iii) For supersonic flow M > 1, V > a and |Aa| > |AV|
(iv) For transonic flow M ~ 1, V ~ a and |Aa| ~ |AV|
(v) For hypersonic flow M > 1, V > a and |Aa| > |A V|
In hypersonic flow, changes in velocity are very small and the variations in Mach number are mainly due to changes in a.











