Similarity Solutions for Power Law Bodies

There is a certain class of self-similar motions for which the partial differential equa­tions reduce to ordinary differential equations, thus leading to a great simplification and in some cases to analytical solutions.

The concept of self-similarity refers here to flow in which the flow variables between the shock and the body are similar to each other at different stations along the body.

The use of unsteady analogy or equivalence principle, implies that a number of self-similar solutions obtained for unsteady flow problems become available for calculating steady hypersonic flows.

Besides the wedge and the cone, another useful solution is for cylindrical pistons having a motion given by r ~ tm, and from which the flow past power law bod­ies may be obtained, see Velesko et al. [52]. Other self-similar solutions include a piston expanding according to an exponential law, r = r0et0, see Sedov [53] and Gusev [54].

The analogy with steady hypersonic flows was developed by Grodzovskii [55], Chernyi [56] and Stanyukovich [57].

Lees and Kubota [58] and Mirles [59] obtained directly similarity solutions of the hypersonic small disturbance equation for axisymmetric bodies.

The earliest work on similar solutions of this type of problems was carried by Bechert [60] and Guderley [61]. Guderley derived the appropriate equations and boundary conditions and then reduced the problem to a single first order differential equation and applied his theory to the problem of implosions. In his work, he gave a detailed study of the various singular points of the governing differential equation.

Following Kubota [62], we shall consider steady solutions of the hypersonic small disturbance equations for axisymmetric bodies.

Let the nondimensional variables f, g, h for radial velocity, pressure and density be functions only of n = r /rs, where rs is the reduced shock radius rs/т, hence

and for flow similarity щ is constant, along the body rb/rs = constant, hence the body is given by rb = C2xm.

The ratio of the body to the shock radius and the variation of the flow variables between the shock and the body can be obtained from the solution of the differential equations.

It is possible, however, to find the values of m for which similar flows may exist by considering the drag of the body. Since the surface pressure pb is proportional to r’s, the drag is given by

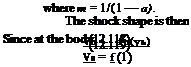(12.120)

D is finite if —2a < 1 + a, or m > 2/(3 + a), where a = 0 for plane and a = 1 for axisymmetric bodies.

The breakdown of similarity for m < 2/(3 + a) does not imply that no flow exists, but only that there is no similarity solution.

Kubota integrated the system of differential equations numerically, for 1 > m > 2/(3 + a), with the corresponding boundary conditions. The drag coefficient for bodies of revolution has a minimum value at m = 0.92, assuming y = 1.4. The distance between the shock and the body decreases as the value of 7 approaches unity. (For y = 1, the shock and the body coincide).

Mirles [59] developed an approximate method based on the asymptotic form of the flow in the neighborhood of the body surface. Both first and second order approximations are in agreement with the numerical solution obtained by Kubota.

The above similarity solutions for power law bodies are limited to the case of strong shocks (M2 в2 > 1).

For a finite Mach number, the solution may be expected to break down towards the rear of the slender body as the shock becomes weaker and the shock angle approaches the Mach angle. Also, the region near the nose of a power law body is excluded since the solutions are based on the use of the small disturbance equations. The similarity solutions for m < 1 predict a density which falls to zero at the body surface. Since the pressure is finite, the entropy will become infinite. Indeed, there is an entropy layer next to the surface in which the small disturbance equations are no longer valid and must be excluded from solutions obtained using the similarity method. For more details see Cox and Crabtree [3].