Subsonic Flow about a Thin Wing

We are going to use the distributed acceleration potential rather than a single one to model the unknown lifting pressure distribution over the wing surface. For this

modeling to work the lifting pressure must go to zero along the trailing edge in order to satisfy the Kutta condition. The lifting pressure as a discontinuity at point (П, g) of the surface is related to the acceleration potential at any point (x, y, z) at time t as follows

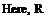(x — n)2 + b2 (y — g)2 + Z2

In Eq. 5.28 the amplitude of the lifting pressure enables us to express the simple harmonic representation in following form.

Dp(n; g; t) = DP(n, g)e“

We know the relation between the lifting pressure and the acceleration potential. Now, we have to relate the velocity potential to the lifting pressure so that we can impose the boundary conditions to obtain the lifting pressure for a prescribed motion of the wing. Equation 2.25 gives the relation between the two potentials. For a simple harmonic motion 2.25 becomes

W = ix/ + (5.30)

o x

Equation 5.30 is a first order differential equation for the velocity potential which has an explicit solution in the following form

x

p = 1 e—ixx/U j W(k, y, z)eixk/Udk (5.31)

Using 5.28 in 5.31 gives us the amplitude of the velocity potential in terms of the acceleration potential as follows

Prescribing the simple harmonic equation of motion for the thin wing as za = za(x, y)eix‘ the boundary condition at the surface reads as

w(x, y)= ix + U0x Pa (x, y)

Integrating the downwash expression over the whole surface S yields

If we substitute 5.32 in to 5.34 we obtain the downwash in terms of lifting pressure as follows

(5.35)

The lifting pressure can be found by solving the integral equation, 5.35, once the boundary condition 5.33 is prescribed as the left hand side of Eq. 5.35. In order to simplify Eq. 5.35 let us define new parameters in terms of the old ones as follows.

x = x — n, y = y — g, x = m/U[f, r2 = b2(y 2 + z2)

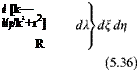Using the new parameters we obtain

The singular inner integral part of 5.36 is subject to a limiting process, and it is called the Kernel function. If we denote the Kernel function with K(x’, y’) and the nondimensional pressure discontinuity with L(n, g) = Ар(П, g)/PoU2 the down – wash expression becomes

= JJL(n, g)K(x, y )dn dg (5.37)

S

Direct inversion of 5.37 is not possible therefore, numerical methods are used for that purpose.