Subsonic Flow Theory

As previously described there are no equivalent exact results that are analogous to Theodorsen’s theory or Wagner’s solution for the unsteady airloads on airfoils in subsonic compressible flow. Here, both the circulatory and the noncirculatory loads have different time-history effect. As shown in Section 8.15 the initial loading on an airfoil operating in a compressible flow can be computed directly using piston theory. For indicial flap

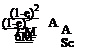motion (i. e., displacements and rates – see Fig. 8.41) about a hinge located e semi-chords downstream of mid-chord, the initial values airloads according to piston theory are

These results are valid for any Mach number, but only at s = 0 when the perturbation (8 or 8) is applied. The final values of the indicial response are given by the linearized subsonic airfoil theory, so that for indicial flap displacements

2 p

ДС„,0=оо, М) = —-ДЗ, (8.233)

f

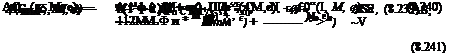The indicial response functions define the behavior between s = 0 and s = oo. The indicial lift, airfoil pitching moment and hinge moment coefficients in response to impulsive flap deflection (about some hinge axis at e) can be written in general functional form as a sum of noncirculatory and circulatory parts, as for the airfoil contributions shown

behavior of the respec­tive indicial airloads between s = 0 and s = 00. The definition of all of these indicial functions is given by Leishman (1994) and Hariharan & Leishman (1996), including the numerical procedures that can be used to manipulate these indicial functions to find the un­steady airloads in response to arbitrary flap motion such as in the recurrence or state-space Grms: