Surface Tension
Liquids behave as if their free surfaces were perfectly flexible membranes having a constant tension a per unit width. This tension is called the surface tension. It is important to note that this is neither a force nor a stress but a force per unit length. The value of surface tension depends on:
• the nature of the fluid;
• the nature of the surface of the substance with which it is in contact;
• the temperature and pressure.
Consider a plane material membrane, possessing the property of constant tension a per unit length. Let the membrane have a straight edge of length l. The force required to hold the edge stationary is:
p = al. (2.11)
Now, suppose that the edge is pulled so that it is displaced normal to itself by a distance x in the plane of the membrane. The work done, F, in stretching the membrane is given by:
F = alx = a A, (2.12)
where A is the increase in the area of the membrane. It is seen that a is the free energy of the membrane per unit area. The important point to be noted here is that, if the energy of a surface is proportional to its area, then it will behave exactly as if it were a membrane with a constant tension per unit width, and this is totally independent of the mechanism by which the energy is stored. Thus, the existence of surface tension, at the boundary between two substances, is a manifestation of the fact that the stored energy contains a term proportional to the area of the surface. This energy is attributable to molecular attractions.
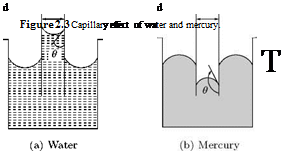
An associated effect of surface tension is the capillary deflection of liquids in small tubes. Examine the level of water and mercury in capillaries, shown in Figure 2.3.
When a glass tube is inserted into a beaker of water, the water will rise in the tube and display a concave meniscus, as shown in Figure 2.3(a). The deviation of water level h in the tube from that in the beaker
 |
can be shown to be:
о
h a cos 9, (2.13)
d
where 9 is the angle between the tangent to the water surface and the glass surface. In other words, a liquid such as water or alcohol, which wets the glass surface makes an acute angle with the solid, and the level of free surface inside the tube will be higher than that outside. This is termed capillary action. However, when wetting does not occur, as in the case of mercury in glass, the angle of contact is obtuse, and the level of free surface inside the tube is depressed, as shown in Figure 2.3(b).
Another important effect of surface tension is that a long cylinder of liquid, at rest or in motion, with a free surface is unstable and breaks up into parts, which then assume an approximately spherical shape. This is the mechanism of the breakup of liquid jets into droplets.











