The Aerodynamic Loads

The solution of Eq. (8.16) will provide the spanwise bound circulation distribution Г(у). To obtain the aerodynamic forces, the two-dimensional Kutta-Joukowski theorem will be applied (in the у = const, plane). However, because of the wake-induced velocity, the free-stream vector will be rotated by

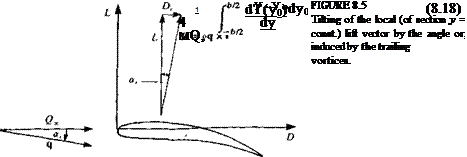a,(y), as shown in Fig. 8.5. This angle can be calculated for a known Г(у) by using Eqs. (8.10) and (8.13):

By assuming that or, is small, then cos a, ~ 1, and sin a, ~ a, and the lift of the wing is given by an integration of the local two-dimensional lift (see Eq. (3.113)) as

гьа

L = pQao Г(у) dy (8.19)

J-ьа

while the drag force, which is created by turning the two-dimensional lift vector by the wake induced flow, becomes

гыг

A = pQ°° ЖуЖу) dy (82°)

■>-ыг

This drag is called induced drag because it is induced by the trailing vortices. This finite wing’s drag is directly related to the lift and will diminish as the wing span increases (b —»°°). Equation (8.20) can also be rewritten in terms of the wake-induced downwash w, :

гЬП

Di = – p w,(y)r(y) dy (8.20a)

■>~ыг

From the engineering point of view, the total drag D of a wing includes the induced drag A and the viscous drag D0:

D = A + D0

For example, the two-dimensional viscous drag of a NACA 0009 section is presented in Fig. 5.19.