Our heavyweight helicopter equal in the world does not have
In Rostov started production of the most load-lifting rotary-wing car The Russian holding «Helicopt[...]
THE DERIVATIVE Сц
 |
Сг is known as the damping-in-roll derivative. It expresses the resistance of the airplane to rolling. Except in unusual circumstances, only the wing contributes significantly to this derivative. As can be seen from Fig. 8.12, the angle of attack due top varies linearly across the span, from the value pb/2V at the right wing tip to —pbj’2 V at the left tip. This antisymmetric a distribution produces an antisymmetric increment in the lift distribution as shown in Fig. 8.13. In the linear range this is superimposed on the symmetric
lift distribution associated with the wing angle of attack in undisturbed flight. The large rolling moment L produced by this lift distribution is proportional to the tip angle of attack p, and <7^ is a negative constant, so long as the local angle of attack remains below the local stalling angle.
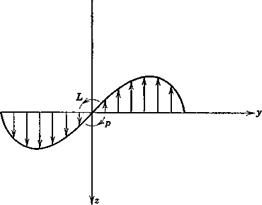
If the wing angle of attack at the center line, a„(0), is large, then the incremental value due to p may take some sections of the wing beyond the stalling angle, as shown in Fig. 8.14. [Actually, for finite span wings, there is
|
Fie. 8.14 Reduction of Сц due to wing stall. |
an additional induced angle of attack distribution ац(у) due to the vortex wake that modifies the net sectional value still further. We neglect this correction here in the interest of making the main point.] When this happens GtJ) is reduced in magnitude from the linear value and if ocw(0) is large enough, will even change sign. When this happens, the wing will autorotate, the main characteristic of spinning flight.
