Trimming the Glider for Maximum Distance

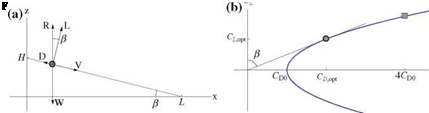
One of the glider design goal consists in achieving the largest distance on the ground, given an initial release point and altitude, assuming a perfectly quiet atmosphere. The situation is depicted in Fig. 11.12a. The glider is released from a height H and will land at point at a distance L. The slope of the trajectory is в, hence the objective is to minimize |в | = D/L. With the simple equilibrium model, and the drag being given by

c L

Cd = Cd0 + ^ (11.63)

n eAR

it is equivalent to minimize D/L or Cd /Cl as

so that the corresponding drag is Cd = 2CD0. Geometrically, this corresponds to the point of contact of the tangent through the origin with the parabola, see Fig. 11.12b.

11.3

Trimming the Glider for Maximum Duration

Another strategy for a glider is to stay airborne the longest time, or maximum dura­tion. This is achieved by minimizing the speed of descend, i. e. for small angles, |w| = V |в|. As pointed out earlier, the equilibrium speed V is proportional to the square root of the weight Vw", but also to the inverse square root of the lift coefficient 1/VCL. Hence |w| ~ CD/C3/2. One obtains

Г C1/2

C DO C t

f (Cl ) = – D + – L,

CJ/2 n eAR

CL

. 3 CD0 1 C-1/2

^ f =– D/2 + L = 0, ^ Cl = J3neAR CD0 (11.65)

2 c5/2 2 neAR

CL

and the corresponding value of drag is CD = 4CD0. This is represented by the square in Fig. 11.12b. Note that to change from maximum distance to maximum duration, the incidence is increased and the velocity decreased. Analysis of the results show that the ratio of the maximum duration time to the maximum distance time is 33/4/2 = 1.14, a 14 % increase in time. The distance achieved is however reduced, in comparison to the maximum distance calculated above, in the ratio /2 = 0.87, a 13 % reduction.