Velocity change across the normal shock

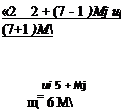The velocity ratio is the inverse of the density ratio, since by continuity u2ju = рі/рг. Therefore, directly from Eqns (6.45) and (6.45a):

Of added interest is the following development. From the energy equations, with cpT replaced by [7/(7 – l)]p/p, pi/pi and pijpi are isolated:

and

P2 7 V 2

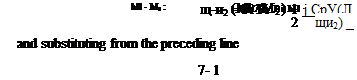The momentum equation (6.37) is rearranged with рщ = piui from the equation of continuity (6.36) to

Disregarding the uniform flow solution of щ = u2 the conservation of mass, motion and energy apply for this flow when

2(7-1) m

uu2=——– rr-CpTo

7+1

cpTo = a*

i. e. the product of normal velocities through a shock wave is a constant that depends on the stagnation conditions of the flow and is independent of the strength of the shock. Further it will be recalled from Eqn (6.26) that

where a* is the critical speed of sound and an alternative parameter for expressing the gas conditions. Thus, in general across the shock wave:

(6.52)

This equation indicates that щ > a* > u2 or vice versa and appeal has to be made to the second law of thermodynamics to see that the second alternative is inadmissible.