Wall Shear Stress at Flat Surface Portions

The wall shear stress tw is the cause of the skin-friction drag, which is exerted by the flow on the flight vehicle. For a CAV this drag together with the form drag can be up to approximately 50 per cent of the total drag. For RV’s at large angle of attack, the skin-friction drag is almost negligible [36]. The wall-shear stress can also considerably influence lift forces, especially during flight at higher angles of attack, and moments around the pitch and the yaw axis. Finally it is a deciding factor regarding erosion phenomena of surface coatings of thermal protection systems of RV’s.

The wall shear stress in the continuum regime and in Cartesian coordi­nates is defined as, see also eq. (4.36)

(7.136)
Tw, lam
In terms of the unit Reynolds number Re^ = pTOuTO/^TO this reads
(7.137)
Tw, la
(7.140)
(7.141)
0.0592 (ЙЄ со,.)0-2
(7.142)
cf, turb
For the reference-temperature extension, density and viscosity in eqs. (7.136) and (7.140) are all to be interpreted as data at reference temper­ature conditions. The equation for the laminar flat-plate boundary layer then reads
	* Ч 0.5 0.5 P И
(7.143)
Tw, lam, c

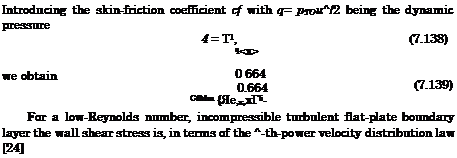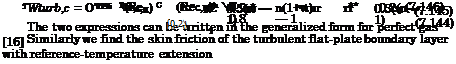We introduce p*T* = pcTc together with the power-law formulation of viscosity. With the nomenclature used for the thicknesses of compressible boundary layers, where the subscript ‘c’ stands for the compressible and ‘ic’ for the incompressible case, we obtain

with C = 0.332 and n = 0.5 for laminar flow, and C = 0.0296 and n = 0.2 for turbulent flow.

An alternative formulation is:

Before we summarize these results, we have a look at the result, which exact theory yields with the use of the Lees-Dorodnitsyn transformation for the wall shear stress of a self-similar compressible laminar boundary layer

[35].

We quote the result in a form given by J. D. Anderson Jr. [37]

The dependence of tw on the Reynolds number is like in eq. (7.144). The function f ‘(0) is the derivative of the velocity function f1 = u/ue at the wall. It implicitly is a function of the boundary-layer edge Mach number Me, the Prandtl number Pr, and the ratio of specific heats 7. Hence we have a dependence like in eq. (7.136) on these parameters, however implicitly and in different form.

Summary. Like for the boundary-layer thicknesses discrepancies can be found in the literature regarding the simple relations for the wall shear stress of two-dimensional incompressible and compressible flat-plate turbu­lent boundary layers. We do not pursue this problem further.

We summarize the results, eqs. (7.144), and (7.145), respectively eq. (7.146), in Table 7.5. We substitute also ‘TO’ conditions by general ‘ref’ con­ditions and choose ш = ш^ = 0.65 in the viscosity law, Section 4.2.[106] We in­troduce the dynamic pressure qref = 0.5 prefv2ef and break up all Reynolds numbers Re into the unit Reynolds number Reu and the running length x in order to show explicitly the dependencies on these parameters.

Table 7.5. Flat surface portions: dependence of boundary-layer wall shear stress on the running length x, the dynamic pressure qref, the unit Reynolds number Re’Uef and the reference-temperature ratio T*/Tref (ш = = 0.65). Wall shear stress eq. X Qref Reref T /Tref 7~lam (7.144) OC :r-°’6 OC Qref ос (Re:“e/)-°-6 – (*ri7‘ £ (7.145) OC :r-°’2 OC Qref ос {Reuref)-°-2 – С*Г’“

The third, fourth and the fifth column in Table 7.5 give the basic de­pendencies of the wall shear stress of both incompressible and compressible boundary layers on the running length x, the unit Reynolds number ReUef and the dynamic pressure qref, the sixth column the dependence of the wall shear stress of compressible boundary layers on the reference-temperature ratio T*/Tref, i. e., on the wall temperature Tw and the Mach number Mref, eq. (7.129).

These dependencies give us insight into the basic behavior of the wall shear stress of two-dimensional flat-plate boundary layers.

— Dependence on the boundary-layer running length x.

The wall shear stress decreases with increasing x. The wall shear stress of laminar boundary-layers reduces stronger (ж x-0 5) with x than that of turbulent boundary layers (ж x-0 2). Remember that the thickness of the viscous sub-layer grows only very weakly with x compared to the thickness of the laminar boundary layer.

— Dependence on the dynamic pressure qref.

The wall shear stress of laminar as well as of turbulent boundary layers increases linearly with increasing dynamic pressure.

— Dependence on the unit Reynolds number ReUef.

The wall shear stress depends on the inverse of some power of the unit Reynolds number. The larger ReUef, the smaller is the wall shear stress. The wall shear stress of laminar boundary layers reacts stronger on changes of the unit Reynolds number (ж (Re^^ )-0’5) than that of turbulent boundary layers (ж (Re^ef )-0 2). This result is not surprising, because the dynamic pressure qо was isolated, see, e. g., eq. (7.146). In the alternate formulation of eq. (7.147) we have ж (ReUef )0 5 for the laminar, and ж (ReUef )0 8 for the turbulent case.

— Dependence on T*/Tref.

Summary. In Table 7.6 the general dependencies of the wall shear stress tw in eq. (7.149) are summarized for laminar and turbulent flow. Again we choose ш = = 0.65 in the viscosity law, Section 4.2. We introduce, like

before, the dynamic pressure qref and break up the Reynolds number Re into the unit Reynolds number Reu and the radius R. Regarding the reference- temperature dependencies the differentiation recommended in [16] for the laminar and the turbulent case (see above) is not made. Instead we write on the basis of eq. (7.150)

The results are:

— Dependence on the dynamic pressure q, x.

Table 7.6. Attachment line at the infinite swept circular cylinder: dependence of wall shear stress Tw, eq. (7.149), of the compressible laminar and turbulent bound­ary layer on the dynamic pressure qTO, the radius R, the sweep angle p, the unit Reynolds number Re^, and the reference-temperature ratio T* /Tx (ш = = 0.65). 7~w, scy Qoo R A Ret, Т*/Т. А 7~w, lam Ж ^oc ж R-°-5 ж sin y(cos p)°’b ж (ад-0-6 / -0.175 *(£) 7~w, turb Ж ^oc ж R-°-21 ж (siny)1′[107](cosy)0’21 ж (ВД-0-21 / т, -0.653 <Х ( TV )

— Dependence on the radius R.

The wall shear stress decreases with increasing R stronger for laminar, ж R-0’5, than for turbulent flow, ж R-0’21.

— Dependence on the sweep angle p.

For p = 0° we have the case of the non-swept circular cylinder (2-D case), where Tw, scy is zero in the stagnation point. For p ^ 90° also Tw, scy ^ 0. This means that the attachment line ceases to exist for p ^ 90° and we get the situation on an infinitely long cylinder aligned with the free-stream direction, where finally rw, scy becomes zero. In between we observe that Tw, scy first increases with increasing p and that stronger for laminar than for turbulent flow. This reflects the behavior of the component we of the external inviscid flow, Fig. 6.37 b), which grows stronger with increasing p than the velocity gradient due/dx across the attachment line declines with it. At large p finally the effect reverses, first for laminar then for turbulent flow, and Tw, scy drops to zero.

— Dependence on the unit Reynolds number ReЦ,.

The wall shear stress depends on the inverse of some power of the unit Reynolds number in the same way as on flat surface portions with ж (ReU)-0 5 for the laminar and ж (Re^)-0 21 for the turbulent bound­ary case. The larger ReU, the smaller is the wall shear stress. Again one has to keep in mind the dependence on the dynamic pressure, which has been isolated in this consideration.

— Dependence on T*/T, x.

At a general three-dimensional attachment line the velocity gradient due/dxx=0 and are not connected explicitly to a geometrical property of the configuration. In any case it can be stated that the larger due/dx, the smaller the relevant boundary-layer thickness, and the larger the wall shear stress. Of course also here the magnitude of we plays a role. tw depends also here inversely on the wall temperature and that, like in general, stronger for turbulent than for laminar flow.