Aerodynamic Derivatives and Modeling

4.1 INTRODUCTION

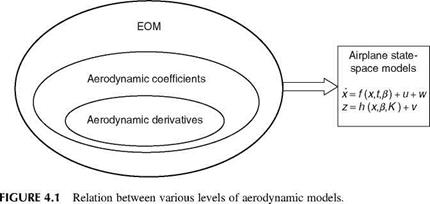
Apart from the equations of motion (EOM) discussed in Chapter 3, the quantification and analysis of aerodynamic models is most important for flight mechanics analysis. The forces and moments that act on an aircraft can be described in terms of aerodynamic derivatives. The stability and control analysis is an integral part of aircraft design cycles, design evaluations, and design of control systems. In this analysis, the aerodynamic derivatives, often also known as stability and control derivatives, form the basic inputs [1-3]. For conventional stable aircraft configur­ations these derivatives directly ensure the required levels of stability and control­lability. For unstable aircraft configurations these derivatives form the essential input parameters for the design of control laws, which in turn ensure the desired stability and controllability characteristics of the aircraft. Stability derivatives also play an important role in the selection process of aircraft configuration, as will be seen in Section 4.4 [4]. This aerodynamic model then becomes an integral part of the EOM that in totality represents the aerodynamics as well as the dynamic behavior of the vehicle. The accuracy of the results of any flight mechanics analysis depends on the degree of completeness and approximation of the aerodynamic models used for such analysis. Due to the assumption of linearity often made, the validity of these models (the EOM and aerodynamic models) is limited to a small range of operating conditions. These operating conditions are generally in terms of the angle of attack (AOA) and Mach number. Often the excursion in the angle of sideslip (AOSS) is assumed to be small. In general, aerodynamic derivatives are applicable to small perturbation motion about a particular equilibrium and this leads to quasi-static aerodynamic derivatives. Large amplitude motions and maneuvers require sophisti­cated and complex aerodynamic modeling. In this chapter we deal with aerodynamic modeling, which basically consists of aerodynamic coefficients that in turn expand to (or encompass) aerodynamic derivatives. Certain stability and control aspects (of aircraft) are captured in certain aerodynamic derivatives. Primary knowledge of aerodynamic coefficients, especially of aerodynamic derivatives, can be obtained from some analytical means like DATCOM, CFD, and wind-tunnel (WT) experi­ments (Appendix A). When flight tests are conducted on an airplane and if they instrumented properly with sensors, one can measure the dynamic responses (p, q, r, AOA, AOSS, Euler angles, and linear accelerations) of the aircraft when certain maneuvers (Chapter 7) are performed. These responses/data can be processed using parameter-estimation methods to obtain the aerodynamic coefficients/derivatives

(ACDs), as will be discussed in Chapter 9. The interplay of aerodynamic coeffi­cients, derivatives, and EOM at the top level is shown in Figure 4.1.