APPROXIMATION

Many useful results and insights can be obtained using the flat-Earth approximation. As we showed in Chapter 5, this approximation is valid for a wide range of flight conditions. We begin with the longitudinal modes, for which the relevant small-disturbance equations in nondimensional form are (5.13,18 and 19). We shall consider first a subsonic transport airplane in a reference steady state of horizontal flight, (ye = 0) and initially neglect the 2 derivatives as well. This is an approximation that is almost universally made in dealing with the flight of airplanes at subsonic speeds. Its significance is explored in Sec. 9.4. Thus the relevant equations are (5.13,19) with ye = 0.

For this class of vehicle there is little error entailed by assuming that the inclination of the thrust vector, otT, is zero, and we make this assumption.

Since we are concerned with stability of a steady state, i. e. with autono­mous behavior, all the elements of the control vector—the last column on the r. h.s. of (5.13,19)—are zero as well. We are left then with an autonomous linear/invariant system with the matrix shown on the facing page.

The general theory for such systems has been given in Sec. 3.3, where it was pointed out that the central elements of the solutions for free motion are the eigenvalues and eigenvectors. To obtain the natural modes of a vehicle, subject to the approximations and restrictions implicit in (9.1,1), it then remains to assign numerical values to the elements of A and to calculate its eigenvalues and eigenvectors.

Numerical Example. The following data pertain to a hypothetical jet transport airplane flying at high altitude.

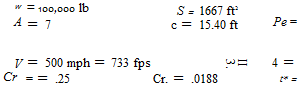60 psf

.000889 (approx. 30,000 ft altitude)

7 /л

.0105 sec C *

CD = .016 + —

7tt

It is assumed that the thrust of the jet engines does not vary with speed, i. e. 3TjdV = 0, and that there are no speed effects on the aerodynamic deri­vatives. The remaining data needed for (9.1,1) are given for this particular vehicle as (see Table 7.1)

0La = 4.88; Cmx=-<t.88(hn-h)-, (A„ – A) = .16 2C

GDa = ~~ GLx’’ GL& = = —4.20

®l, — 0; Oma = – 22.9; GTv=-2GTe=-2CDe CLr = CDy = Gmf = 0.

Using the above data, the coefficients of A were calculated, and the eigen­values and eigenvectors found by library subroutines’}- available for the UTIAS IBM 1130 computer. Let the eigenvalues be X — n і ico where the denotes nondimensional values (note that the independent variable of the differential equations is t = t/t*). The properties of interest are then, in real time:

Period, T = t* —

ft)

-^half — ^half/^1

The results obtained are as follows: