Our heavyweight helicopter equal in the world does not have
In Rostov started production of the most load-lifting rotary-wing car The Russian holding «Helicopt[...]
Axisymmetric Longitudinal Flow Past a Slender Body of Revolution
The axisymmetric version of Laplace’s equation (Eq. (8.105)) is
Э2 Ф Э2 Ф 1ЭФ dx2 + dr2 + r dr
and the body boundary condition is given by Eq. (8.108a). The solution is modeled by a distribution of sources of strength o{x) per length along the body axis on the strip О^лг £/, z — 0 (Fig. 8.26) and the problem is essentially the axisymmetric version of the two-dimensional thin-airfoil thickness problem. The perturbation velocity potential and velocity components for this distribution are obtained by integrating the equations of the point source (see Section 3.4) along the x axis:
|
= Ґ o(x0)dx 4л Jo V(* – Xq)2 + r2 ЭФ = J_ Ґ o(x0)rdx0 dr 4л Jo [(* – x0)2 + r2]3’2 |
(8.110)
(8.111)
ЭФ_ 1 Ґ o(x0)(x — x0) dx0 qAr, X) dx 4ло[{х-Хд )2 + г2]ш
To satisfy the body boundary condition (Eq. (8.108a)), which states that the flow is tangent to the surface,
^- = Rx) at r = R
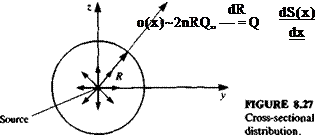
we use the slenderness arguments developed in slender wing theory and consider a mass balance in the crossflow plane (see Fig. 8.27). Surround the body axis with a circle of radius r and the volume flow (per unit length, Ax) through this circle is equal to the source strength
 |
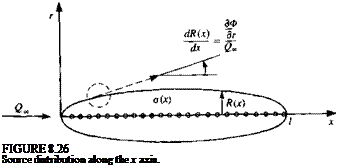o(x) = 2nrqr (8.113)
 |
 |
If Eq. (8.113) is evaluated at r = R and the boundary condition of Eq. (8.108e) is used, the source strength is found to be
 |
 |
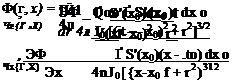where S(x) is the body cross-sectional area. The potential and velocity components are then found by substituting o(x) into Eqs. (8.110-8.112),
