Our heavyweight helicopter equal in the world does not have
In Rostov started production of the most load-lifting rotary-wing car The Russian holding «Helicopt[...]
Boundary layer calculation methods
The next most reliable method of profile drag prediction is to actually perform the boundary layer calculations to obtain the far-downstream or KTO. However, this can run into difficulties if a simple classical boundary layer calculation is used, since the ue(s) distribution from a potential solution typically has a very
steep adverse pressure gradient immediately ahead of the trailing edge stagnation point. Consequently the classical boundary layer calculation will fail there due to the Goldstein separation singularity, as discussed in Section 4.12.1. The fully-coupled viscous/inviscid XFOIL and MSES methods avoid these pitfalls by allowing ue(s) to adjust in response to the viscous displacement, which removes the Goldstein singularity.
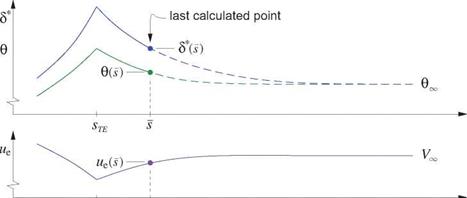
The boundary layer calculation can be stopped at the trailing edge, or continued into the wake if ue(s) is known along the wake. This raises the practical problem of how to determine or dTO from d(s) at the last calculated point X, which may be either at the trailing edge or at the end of a wake of finite length. A suitable method is to use the von Karman equation (4.28) which in the wake simplifies as follows.
– ГТТ, O’ 1 dt;e d ds 1 + ’ ue ds
d(ln d) = —(H + 2) d(ln ue) (in wake) (4.116)
This can be approximately integrated from the last known location s = s to far downstream s if we assume an average value of Havg over this interval. Since H ^ 1 far downstream in an incompressible wake, a reasonable approximation is
tfavg ^ (4.117)
 |
 |
 |
 |
so that equation (4.116) then explicitly gives dTO in terms of the known quantities at s.
The relations are diagrammed in Figure 4.29. Equation (4.118) is known as the Squire-Young formula [34], and was originally developed for cases where ss is at the trailing edge, so that the extrapolation is over the entire wake. However, it can be used if s is some distance downstream in the wake, and in fact it then becomes more accurate because the H ~ Havg assumption then gets better.
s
The Squire-Young formula is also useful in experiments, where it can be used to extrapolate a measured wake momentum defect near the airfoil to downstream infinity, so that the actual profile drag can be determined from the measurements. This is described in Section 10.4.2.
