Comparison with Measurements

The preceding theoretical development applies to flaps that do not lose their ef­fectiveness because of viscous effects. In practice a trailing edge flap may operate in a relatively thick turbulent boundary layer because the flap hinge produces a locally adverse pressure gradient that tends to thicken the boundary layer. This will alter the effective flap camber, reducing the flap effectiveness for a given flap deflection angle – see White & Landahl (1968). In addition, the influence of the flap hinge geometry and the possibility of a gap at the hinge leads to additional viscous effects that may adversely alter the re­lationship between the flap deflection angle and the aerodynamic forces and moments – see Gray & Davies (1972). To a first order it is possible to account for such effects by the application of flap effectiveness coefficients. However, because the lift, moment, and hinge moment will be influenced to different degrees by viscosity, the effectiveness of each component of the loading must be considered separately. Flap effectiveness coefficients can be derived most accurately by empirical means on the basis of quasi-steady flow con­siderations; that is, based only on circulatory effects and with regard to measurements of the aerodynamic coefficients at very low reduced frequency with flap angle and gap size. Therefore, the actual aerodynamic forces and moments will be the linear theory values mul­tiplied by constant terms, say en,€m, and 6/,, which may be functions of Reynolds and Mach number.

Experimental results for a NAC A 64A006 airfoil with an oscillating plain flap are reported by Tijdeman & Schippers (1973). The main emphasis in this work was for the high subcritical and transonic flow cases, but results are given for shock-free flow and weak transonic conditions. Under these conditions nonlinear effects are relatively mild and the results can be expected to provide a useful basis for comparison with the foregoing incompressible and compressible flow theories. Some additional results for an oscillating flap on a NLR 7301 airfoil are given by Zwaan (1982a, b), although these data are more limited. From the equations given previously, the response to a particular harmonic motion of the flap can be derived.

Representative results are shown in Fig. 8.42 for two conditions, one at the lowest Mach number of 0.5 and the other for M = 0.748. Also included in these plots are results from the incompressible theory, but with the lift curve slope corrected by the Glauert compressibility factor 1//3. When plotted versus flap displacement angle, as shown in Figs. 8.42(a) and (b), the lift coefficient curve exhibits a characteristic elliptical loop that is similar to that obtained on an airfoil oscillating in angle of attack. A flap lift effectiveness of e„ = 0.70 was determined from the real part of the aerodynamic response at zero frequency and this value was assumed to be constant over the entire Mach number and frequency range. Notice that in Fig. 8.42(a) and (b) the lift loops are circumvented in a counterclockwise direction, corresponding to a phase lag. At higher flap oscillation frequencies, the lift will develop a phase lead as the noncirculatory terms begin to dominate. However, the effects of increasing free-stream Mach number tends to increase the circulatory lag, which means that the lift mostly lags the flap forcing over the range of conditions typically encountered in practice. This is shown for the M = 0.748 case in Fig. 8.42(b), where despite the higher reduced frequency the phase lag is considerably greater. Notice that the incompressible results do not correlate as well with the experimental results; the incompressible theory does not predict the phasing correctly at the Mach numbers typical of helicopter rotors.

Figures 8.42(c) and (d) show that the airfoil pitching moment behaves in an almost quasi-steady manner. A value of em = 0.96 was found to be applicable for this component of the loading. Here, the pitching moment loops are circumvented in a clockwise sense,

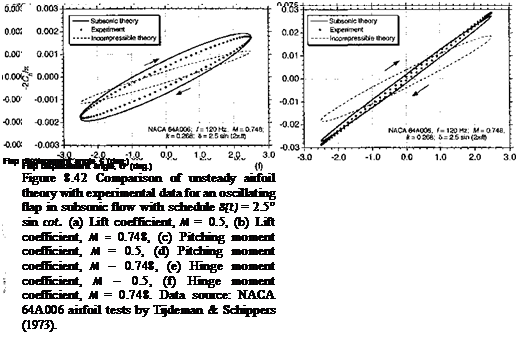but the phase lead is small. In general, there is a weak effect of both Mach number and frequency on the unsteady airfoil pitching moment, and it would be adequately predicted in the general case if quasi-steady conditions were assumed. Figures 8.42(e) & (f) show that the flap hinge moment experiences a considerably more powerful unsteady effect. This proponent is probably the most difficult quantity to predict accurately because it is sensitive to viscous effects; the flap airloads are strongly influenced by the local geometry and pressure ‘ gradients produced near the flap hinge. As discussed previously, such effects are usually corrected for empirically and a hinge moment effectiveness of €h — 0.68 was inferred from e quasi-steady aerodynamic data for this airfoil section. In this case there is a phase lead

between the response and the forcing, giving loops that are circumvented in a clockwise direction. Again, this is because of the noncirculatory terms, which play an important role in determining the aerodynamic response at higher flap frequencies. In this case, even when the free-stream Mach number is low, the disturbances do not propagate sufficiently quickly relative to the flap motion for the flow to be considered as incompressible.