Hypersonic Vehicle Design

Townend [156] considered three applications:

(i) space launchers with reusable aerospace planes,

(ii) hypersonic airlines,

(iii) trans-atmospheric orbital transfer vehicles.

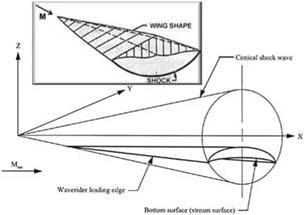
In all three applications, a central theme is integrating air-breathing propulsion into an aerodynamic design called “waverider”, a concept introduced by Nonweiler [157]. The idea is to generate three dimensional lifting bodies in high Mach number flows utilizing the streamlines behind a known shock wave.

It is well known that the maximum lift to drag ratio, (L/D)max, decreases as Mach number increases in the hypersonic regime, due to the strength of the shock wave. As an example is the dependence of L/D versus angel of attack for a flat plate, according to Newtonian flow theory. Accounting for laminar skin friction, (L/D)max is 6.5 for M0 = 10 and Re = 3.0 106. For a Boeing 707 cruising near Mach one, (L/D)max ~ 20. To generate higher L/D, waveriders are considered (see Anderson [9], Hayes and Probstein [2]).

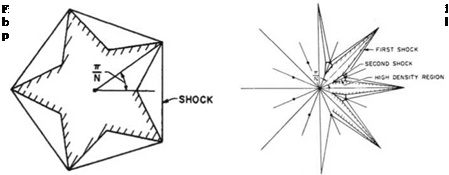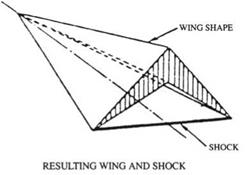
Fig. 12.19 Nonweiler caret wing

Inviscid flow solutions for star-shaped conical bodies using wedge solutions have been given by Maikapar [158] and Gonor [159]. See Fig. 12.18 for the cross section of the body and the shock system.

Such a design may have much less drag than a circular cone of the same cross section area.

Nonweiler [157] and Peckham [160] have proposed delta wings of inverted V-shape, which can be considered as pieces of Maikapar’s shape.

The shock waves in Maikapar’s solution are weak. In Gonor’s solution, a straight weak shock is reflected from a plane of symmetry, in a regular manner and strikes the arm of the star.

An example of Nonweiler wing and shock known as “caret wing” is shown in Fig. 12.19.

The flow over a cone at zero angle of attack can be used to generate waverider shapes. as done by Jones et al. [161]. See Fig. 12.20 constructed by Anderson [162].

Surveys on waveriders are given by Townend [156], Eggers et al. [163], Kuche – mann [18], Roe [164] and Koppenwwalter [165].

Fig. 12.20 Bodies supporting and containing parts of conical shock waves (from en. wikipedia. org)

Recently, Sobieczky et al. [166] introduced inverse aerodynamic design meth­ods to obtain more general shapes of waveriders from given shock waves. In this approach, a flow field bounded by a shock wave, a stream surface defining a solid body contour and an exit surface are calculated. For 2D inviscid supersonic flow, marching in the flow direction or normal to it are both possible. For three dimensional flows, cross marching is an ill-posed problem. However, axisymmetric equations can be used to approximate (to second order) locally three dimensional flows. Location of the axis of this “osculating” axisymmetric flow depends on local flow curvature and velocity gradient. The calculations can be made in a 2D meridian plane by the method of characteristics, however occurrence of limit surfaces (with multi-valued solution) requires initial data modification. Alternatively, the authors solved Euler equations in an inverse approach, guided by characteristic domain of dependence.

Rasmussen and Stevens [167] were able to use calculus of variations to optimize the waverider shapes utilizing the available analytical solutions and the associated properties of inviscid flow. In this regard, the reader is referred to the book on optimum aerodynamic shapes edited by Miele [168].

Recently, Cole [169] designed optimal conical wings in hypersonic flows based on Euler codes.

Long [170] studied the off design condition performance of hypersonic waveriders using Euler codes.

In the above works, skin friction drag is not included, hence the inviscid L/D is not reliable since the waveriders have large wetted surface areas. Anderson [9] introduced a family of waveriders called viscous-optimized hypersonic waveriders using CFD code and numerical optimization techniques. Comparison with wind tunnel tests are satisfactory. Their designs differ considerably in shape, depending on laminar to turbulent transition models. Anderson [9] considered also nonequilibrium chemistry on waverider aerodynamics. Nonweiler [157] raised the concern whether the sharp leading edges of waveriders can survive the heat flux without using active cooling. With the available new materials, the solid body conductivity and radiative cooling can indeed limit the temperature to acceptable levels.