INFLUENCE OF THE SLIPSTREAM UPON THE VERTICAL TAIL

The slipstream of the propulsion system has two particu­lar characteristics. It has an increased dynamic pressure; and it changes to a degree, the direction of flow when sideslipping.

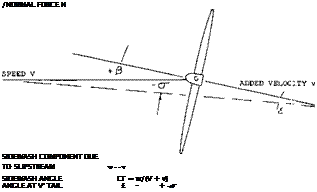
Sidewash. In propeller-driven airplanes, the vertical tail surface is usually located within the slipstream. The tail is thus exposed to a certain destabilizing sidewash and to a stabilizing increase of dynamic pressure. For example, at Tc = 1, the added velocity is v ^ 0.4 V. As demonstrated in figure 30, the sidewash component of v, corresponds to

w/v =

where /3 – angle of sideslip in radians. The maximum possible reduction of the sidewash angle against the axis of an isolated propeller, will then be

<r = W/(V + v) = – /9 (v)/(V + v);

(23)

<Wd/9 = – 1/(1 + (V/v)) = (l//l +)- 1

(26) Influence of dorsal and similar fins:

b) Recant, Curtiss XP-62 Model, W’Rpt L-779 (1943).

c) Wallace, Curtiss XBTC-2, NACA W’Rpt L-787 (1944).

d) Ventral fins (at low R’number), see (33,d).

e) Hoggard, Fuselage with Dorsal Fins, NACA TN 785 (1940).

f) Queijo, Damping Fins,-NACA TN 3814 (1956).

For very small values of thrust, the sidewash derivative is simply dcr/dfl = — 0.5 Tc. For Tc = 1, as mentioned above, theory expects:

dcr/djS =- 1/(1 +2.5) = -0.28

so that the effective angle at the vertical tail might be reduced (in this particular case) to (1 — 0.28) = 0.72. A survey of the flow at the location of the vertical tail surface of a low-wing airplane is shown in figure 27:

a) Without power (with dynamic pressure at the tail, essentially = q) the previously discussed type of cross flow is seen taking place over the upper edge of the fuselage. The maximum sidewash angle is about 1.5 times the angle of sideslip; and it is symmetrical to the two sides of sideslip.

b) In power-on condition (thrust coefficient TG = 0.8) it is evident how slipstream rotation adds a component to the right, in the direction where the blades sweep through the upper half of the propeller circle.

c) As a consequence of (a) plus (b) there is a strong sidewash to the right, when sideslipping to the left, amounting to between 5 and 20 , or 0.5 and 2.0 times the angle of sideslip.

The reduction of the sidewash angle due to slipstream (tested, but not directly evident in figure 27) is in the order of d&jdfi = — 0.11 for Tc = 0.8, and at CL = 0.9. This decrement is in the order of 1/2 of what is predicted in equation (23). It appears that the slipstream does not retain its original direction (if it ever reaches the sidewash angle as expected theoretically). Tentatively, we may thus write:

с1<У /dfi = – 0.5 (1/1 + Tc) – 1) (24)

Dynamic Pressure. The lateral force produced in the verti­cal tail should correspond to

dC^ Id/S = (dCы Idj3)a (1 + do fdp) (q /q) (25)

where (dC/dfi) is meant to be the lateral force deriva­tive of the vertical tail without slipstream, but while attached to the fuselage. For the dynamic pressure (20) at the vertical tail:

q^/q = 1 + Tc (26)

An average value for к is 0.5 when considering horizontal tail surfaces. According to the tests in (21,e) it seems, however, that the vertical surface of an airplane such as in figure 27, is located in that part of the upper half of the slipstream where its velocity is higher. Therefore, a con­stant к = 0.8 may be used in the equation. For example for a set of parameters

Tc = 1.0; dcr dfi = — 0.15; q//q=1.8

the lateral force in the tail and/or the yaw moment contribution by the vertical surface, can be expected to be increased by the factor

(1 + dcr /d^Xq^ /q) = (1 – 0.15) 1.8 = 1.5 (27)

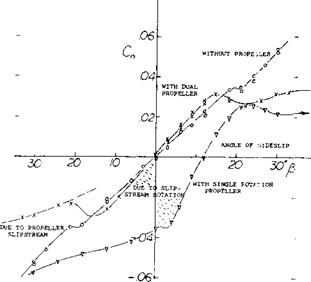
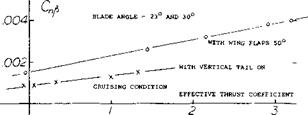
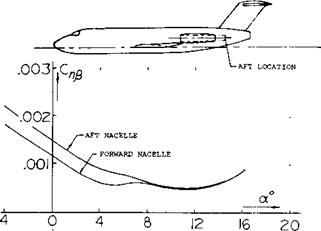
Factors of this type have been evaluated in (22,e). They seem to agree with equations (24) (26) (27). The analysis also agrees fairly well with what is reported in (22) on airplane models using dual-rotating propellers (where the slipstream is symmetrical, without rotation). For example, directional stability of the fighter airplane as in figure 31, is doubled on account of slipstream, in climb condition (full power with Tc = 1.4, at CL = 1.3). This statement should not be misunderstood, however. Stable yaw – moment derivatives of that airplane are as follows:

dCft/d/3 =0.0018 without the propeller (figure 32)

= 0.0011 with propeller, idling = 0.0024 with full power (figure 32)

flaps neutral flaps deflected

of = 12° CL = 1.3 T(; =1.4 Figure 31. Yaw moments of the single-engine airplane as in figure 3, with single and dual rotation propeller (22,a).

dC^/d/S dC-nld/3 0.0018 0.0028 0.0019 0.0053 = 0.15 =0.90

a) low wing windmilling constant power on with Tc b) high wing windmilling constant power on with Tc

0.0011 0.0012 0.0011 0.0030 = 0.15 =0.90

Directional stability of the low wing configuration is al­ways higher than that in high wing arrangement.

2×3 BLADED DUAL ROTATION PROPELLER 50° fuLl-span SLOTTED WING FLAPS 23° BLADE ANGLE AT TAKE-OFF 30° BLADE ANGLE WHEN CRUISING 1/8 SCALE MODEL TESTED, AT Rc = 7 (1C))6 W’RPT L-787

Wing Flaps. Flow conditions at the tail are also a function of the airplane’s angle of attack. Because of the wake developing along the back of the fuselage, and behind the canopy, the effective dynamic pressure and the stabilizing contribution of the vertical tail can be expected to reduce, as the lift coefficient is increased. In wind-tunnel models, at low Reynolds numbers, such as in part (A) of figure 32 for example (where Rc = 6(10) ) the loss in tail effective­ness can amount to 50%. This weakness within a few degrees around zero angle of yaw, disappears however, when deflecting the wing flaps. The angle of attack of the fuselage is evidently reduced in this case. A beneficial effect of flaps is also found in the airplane configuration discussed above (as in figures 31 and 32). With flaps down, the yaw-moment derivatives are some 20% higher. It seems that the flaps make a low-wing configuration even more “low”, and a high-wing arrangement less “high”. It is thus assumed that the favorable sidewash at the location of the vertical tail (above the fuselage) is increased when deflecting the flaps. This conclusion is confirmed in the upper part of figure 34 where the sta­bility derivative is seen increasing as a function of the thrust coefficient. In the condition with wing flaps down, the differential due to vertical tail is about 1/3 larger than in cruising condition (where the flaps are in neutral posi­tion). As a further example, stable yaw-moment deriva­tives are quoted for the two airplanes, as in figure 13:

(A) in cmising condition, (B) with flaps down and take-off power.

(28) The same B-28 airplane as in figure 39, is discussed in the second “longitudinal” chapter. (29) Staufer, Twin Vertical Tail Forces, Ybk D Lufo 1940 p. 1,383. For the horizontal tail of Do-217, see Ybk 1942 p. 1,208.

Inverted Flight. Another consequence of flap deflection is the fact that the asymmetric type of yaw moment func­tion as in figures 29 and 31, is reduced considerably. It seems not only the wing plus flaps take out part of the slipstream rotation; the slipstream also may be deflected down so far that the vertical tail is no longer affected very much. This conclusion is borne out by tests; (31) on a low-wing airplane when flying upside down. In this in­verted attitude (at oL – – 10° for CL = 0.7, for example), the vertical tail surface is below and essentially out of the slipstream. Directional stability is about the same, accord­ingly, as in power-off (windmilling) condition.

-.002-

і і

0.32 SCALE MODEL OF 2300 HP FIGHTER TYPE TEST CONDITIONS: b = 15 ft S = 38 ft2 d 4 ft О 0 – CL = .15 – CTp ^ -00 – Rc = 4’106 23° = BLADE ANGLE 27% SOLIDITY Sp = .33 S

004- Cn

WING + FUSELAGE O’ WITHOUT PROPELLER, сґ’

0.02-

Jet Propulsion. The use of jet engines for propulsion has eliminated many of the directional stability problems en­countered with propeller driven airplanes. For instance there is no direct slipstream effects on the tail as the engines are located so that the tail surfaces are not washed by the hot efflux of the engines. The location of the engines of the airplane do influence the flow at the tail surface however and thus effects the directional stability derivative, Ct2^. For instance the fore aft location of the engines relative to the vertical tail changes as a function of the angle of attack (32). This variation is caused by the cross flow over the fuselage and engine nacelles and is illustrated on figure 35. As found in the arrangement as in figure 36, there can be certain interference effects, however. When at an angle of yaw, the air passing through the engines gets deflected laterally. The consequence is a lateral force AY which can be calculated on the basis of the engine mass flow. De­pending upon the longitudinal position of the engine ducts (in relation to the airplane’s CG) the resulting yaw moment can be “positive” or “negative”. For the airplane as in figure 36, the moment should be expected to be destabilizing. The experimental result is a small stabilizing increment, however. Analysis suggests that a stabilizing force is induced in the particular configuration consid­ered, in the vertical tail. It seems that the presence of the pair of jets makes the configuration more “low wing”, thus inducing some stabilizing sidewash at the location of the vertical tail.

ANGLE OF SIDESLIP

Figure 33. Yaw moments of a fighter airplane tested ( 22,a) with single and dual rotation propeller.

(30) Twin-engine airplanes on one propeller; a) Douglas, After Engine Failure, J. Aeron. Sci. 1935 p. 132. b) Hartman, One One Engine, NACA TN 646 (1938). c) Schmidt, Multiple-Engine Control, Ybk D Lufo 1943, Rpt IA-030. d) Pitkin, B-28 on One Engine, NACA W’Rpt L-191 (1945). e) Goodson, Influence of Thrust Reversal, TN 2979 (1953). (31) Characteristics of fighter-type airplanes, flight-tested; a) Goranson, Qualities of F-47 Airplane, NACA TN 2675 (1952). b) Johnson, Rudder and Sideslipping Curtiss P-40, W’Rpt L-547 (1942). c) White, North American P-51 “Mustang”, W’Rpt L-566 (1943). d) Johnson, Flying Qualities Bell P-39, W’Rpt L-602 (1943). (32) Ray Effects of Large sideslip angles on stability of “T” tail configurations NASA TM X-1665

So far, primarily yaw-moment and other derivatives have been presented and discussed as they are found at and around zero angle of sideslip, say within plus-minus 10 . When going beyond such limits, two changes take place:

1) the vertical tail surface may stall,

2) the tail may “drop” out of the propeller slipstream.

These events and their influence upon stability and con­trol are as follows.

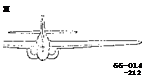
Flow Separation. The only problem regarding the direc­tional characteristics of the jet-propelled airplane in figure 36, is a strong reduction of the derivative dC^/d^S from 0.008 to 0.003, in landing condition (wing flaps down 45 , engines “inoperative” as in the wind tunnel). It seems that there are a pair of separated spaces behind the two engines attached to the sides of the fuselage, thus reducing the dynamic pressure at the vertical (and hori­zontal) tail surfaces.

BELL P-59 TWIN-JET FIGHTER US FIRST (1942) JET AIRPLANE

SEEN FROM BEHIND ___________

b = 45.5 ft ‘

S = 386 ft2

W = 12000 lb

T = 2 2000 lb

Vx = 360 kts

Sy = 8% S

fv = 0.43 b

AS TESTED IN FULL SCALE TUNNEL

dCy/d£ = 0.0050 IN ALL CONDITIONS

dCn/d£ = 0.0008 IN CRUISING CONDITION

= 0.0003 WITH FLAPS 45° AND

ENGINES INOPERATIVE

W’RPT L-626

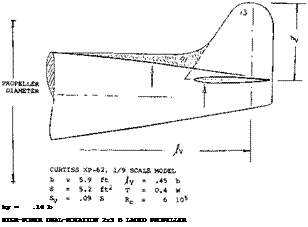
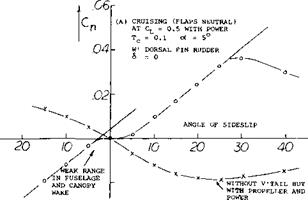
Fuselage. Shown in the Chapter XIX a “second” non­linear component of lift, cross-wind or normal force devel­ops on streamline bodies at the longer angles. Since the location of this lift component is somewhere in the after­body, the corresponding yaw moment about the CG of a typical airplane (located, say at 1/3 of the fuselage length) is stabilizing. The directional characteristics of propeller driven fighter-type airplane are presented in figure 28. Without power, and without vertical tail, the yaw moment derivative dC^/d/3 of the configuration reduces from the original value of – 0.0007 or – 0.0008, to zero at = plus or minus 20°; and it then turns stable reaching comparatively large slopes around and beyond fo = plu&-or minus 40°. There may be some component of yaw mo­ment included in the tested function, caused by the roll moment in the wing, due to yaw. Neglecting this compo­nent, the non-linear differentials tentatively lead to a moment arm of the normal forces in the fuselage

-4/Ь=ДсуДСу =0.30 or = 0.35

This distance from the CG of the airplane ahead of the tail surface, in the middle of the dorsal fin, would appear to be reasonable for the non-linear component of the fuselage’s lateral or normal force.

Figure 36. Directional stability derivatives of Bell P-59, first U. S. jet airplane as tested (24,a) in the Full Scale Tunnel. [123]

Displacement. In Chapter XII it was shown how the propeller slipstream is cut in two parts are displaced in lateral direction, as a consequence of torque and rotation, the upper “half’ to one side and the lower one to the other side. If looking at the airplane in figure 29 .from ahead, the propeller is turning counter clockwise, a right hand prop. Since the configuration is that of a low wing (with most of the propeller disk above the wing) the slipstream is displaced to the side into which the tail moves at negative angles, left on the graph. On this side, therefore, the slope of the yawing moment contribution of the vertical surface has a large increase. On the

other hand, when sideslipping to the other side (to the right in the graph) the derivative is reducing to and below zero. When trimming the airplane by deflecting the rudder so that = zero, the airplane is still stable directionally, at and near ^ – 0. However, at and beyond / = + 6°, as in part (B) of figure 28, that is when sideslipping to the left as seen by the pilot the airplane becomes unstable. The same type of slipstream displacement is also respon­sible for the asymmetry of the sidewash distribution in figure 27, in power-on condition.

Slipstream As noted above slipstream rotation causes the unfavorable asymmetric condition shown on figure 28. This is eliminated on normal jet propelled airplanes as the design is set up so the slipstream does not impinge on the tail. Slipstream rotation is also eliminated by the use of dual rotation propellers or with the use of ducted fans designed for peak performance using vanes to eliminate the rotational losses.

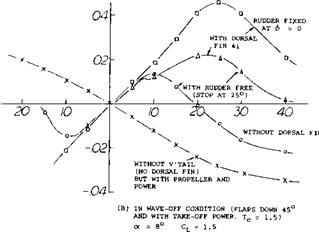
Tail Stalling. Vertical surfaces do stall, at higher angles of yaw however, together with the aft end of the fuselage high stabilizing are still obtained. The reasons why an airplane as in figure 32 turns highly unstable at yaw angles beyond plus/minus 20°, are other than stalling:

a) the vertical tail moves out of the propeller slipstream laterally,

b) the destabilizing normal forces in the propeller is high,

c) there is a considerable destabilizing interference be­tween slipstream and fuselage.

When leaving the rudder alone (not shown in figure 32) a definitely unstable condition is obtained, at ~ plus or minue 10° . In the case of tiem (c) it appears that the slipstream reduces considerably the stabilizing non-linear lateral-force component of the fuselage. This interaction will be discussed after explaining the mechanism of dorsal fins.

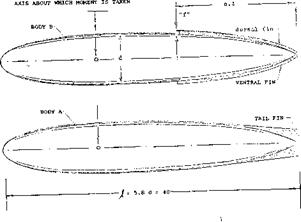
Dorsal Fins. While sideslip angles up to plus-minus 20° seem to be sufficient in any normal operation of the airplane, the loss of restoring forces and moments at larger angles might be dangerous when spinning the airplane. A device expected to improve the directional characteristics, are dorsal and/or ventral fins. Fins of the type as in figure 37, do not have any effect on the yaw moment of the fuselage body, within the range of plus-minus 3 angle of yaw.

BODY "B" HAS THE SAME CONTOUR AS THE ONE SHOWN WITH THE TAIL FIN ATTACHED, ENDING IN A SHARP VERTICAL EDGE.

BODY VOLUME V = 0.61 ft3 = 0.14 J2 = 0.80 d2/ REYNOLDS NO. Rj = 2+ 106

without dorsal and ventral fins (28,a).

Between = 10 and 50 or 60°, the stabilizing influence of the fins in figure 37 is considerable. The principle by which they work, is to increase the fuselage’s “natural” non-linear normal or lateral-force component.. This cross – flow component explained in Chapters III and XXI, is basically of the type

CN^ sin8 oC ; or Су ~ sin2^ (28)

In the extreme, the rear end of the fuselage may be thought of being converted by the addition of dorsal and ventral fins, into a “flat plate”. We have estimated the yaw moment of the body in figure 37, assuming that a lateral area aft equal to 0.4 of the body’s area be a plate, with an aspect ratio of 0.5 and an average moment arm to the yaw axis at 0.32/ , equal to 0.4 of the body length / . Using normal forces as in the Chapter III, the uppermost curve in the graph is thus obtained. Evaluating the experi­mental results in (26,a) with the aid of equation (28), it is found that the “ridges” change flow pattern and cross – flow drag coefficient of the sections of the fuselage to which they are attached. Considering in figure 37, a single point, at = 30° , where sin2ft = 0.25, the lateral force can be expected to correspond to the coefficient based on projected lateral area

CNa = 0.35 = C0a sin2/? = CDa 0.25 The resultant cross-flow drag coefficient of the part of the fuselage “covered” by the fins is CDo = 1.4. After sub­tracting some value for the plain fuselage, the component attributable to the presence of the fins may be A CDa =

1.0. The height of these fins in figure 37, is 5% each of the maximum body diameter. Their combined lateral area is about 13% of the portion of the fuselage “covered” by them SF. We will assume that CDci be proportional to that area ratio. Thus

ACDd =8(Sd/S,-) (29)

Dividing ДС^/ДСу, the center of the lateral force pro­duced in figure 37, is found roughly to coincide with that of the fins.

Airplane Configuration. Dorsal fins have been tested as a means of improving the characteristics of several airplanes (26). As an extreme example, yaw moment characteristics are shown in part (B) of figure 38 of an airplane for the cases of a high powered dual-rotation propeller, and with the rudder free to move.

Directional stability starts to deteriorate at plus or minus 10 angle of yaw. If left alone, the airplane would seek a point of balance beyond 40 . As stated before, the con­tribution by dorsal fins to directional stability in more or less straight flight around. fo = zero is negligibly small. In fact, by disturbing the cross flow around the leading edge of the vertical tail surface, the derivative, , can even be reduced when adding a dorsal fin, although a ventral fin (at the lower side of the fuselage) would probably be somewhat beneficial. The fin as shown in the illustration can be analyzed, using equation (29). In doing so, it must be taken into account however that:

1. the low wing increases the cross flow (some‘30%),

2. the slipstream reduces that flow (some 20%),

3. the dynamic pressure along the fuselage is increased (equation 26).

For the yaw-moment differential A Cy = 0.085, as at P – 40°, a lateral drag coefficient ACDd is thus obtained, which is similar in magnitude to that as found above for the fin in figure 37. Assuming this coefficient, the lateral force contribution of the dorsal fin is figure 38, can be estimated to be

ДСу =(SD/S)(sin^e.)(q^/q)ACDD (30)

where /5. = effective lateral angle = j3{ + d<f /dft). The moment arm of this force fn = 0.28 b, corresponding to /Ь = ДС7?/ АС у is indicated in the drawing.

VERTICAL TAIL CONTRIBUTIONS:

0.0019 CRUISING, TQ = 0.1

= 0.0022 CLIMBING, Tc = 1.0

•• = 0.0021 LANDING, WINDMILLIN3

•’ = 0.0020 AT CT = 2.0, T = L.3

L c

BOTH PROPELLERS TURNING RIGHT

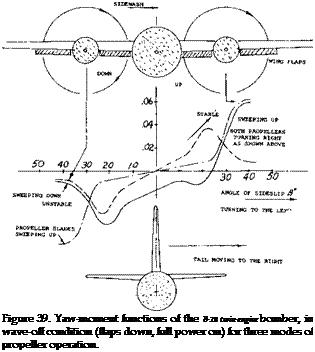
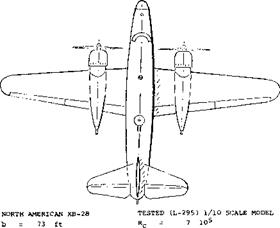
Figure 39. Yaw moment characteristics of the twin-propeller B-28, tested (27 ,c) in a powered wind-tunnel model.

Propeller Moment. It was found above, in part (A) of figure 32, that the destabilizing contribution by a pow­ered propeller grows with the angle of yaw at a rate higher than linear. The explanation is contained in equation (30) where the lateral force due to dorsal fins (or that originat­ing in the tail end of the fuselage body) is seen to be proportional to the square of Д =J3( 1 + dor’ /d/5). In other words, since d& fdft due to slipstream is negative, the stabilizing contribution of the fuselage can easily be reduced. For Tc = 3.1, as in figure 32, equation (23) yields a d(T/d/3 = – 0.5. At /5 = 30°, thus Д = 15°, so that the stabilizing component of the fuselage is reduced to 1/4. It can be concluded that single-propeller airplanes reach a practical limit as to their power, say corresponding to Tc = 2 or 3, beyond which they may no longer be “manageable” when sideslipping.

Twin Propellers. Directional characteristics of the twin engine aircraft are tabulated in figure 38. Within the range of jB – plus-minus 10°, results can be generalized as follows:

a) the normal force of the propellers (with power, corre­sponding to Tc = 1.3, but not shown in the illustra­tion) is almost as large as that of the tail surface,

b) power does not have a noticeable influence upon the fuselage contributions,

c) power does not seem to have an effect upon the contributions by the vertical tail surface,

d) deflection of the wing flaps considerably increases (not shown in figure 39) the lateral force in the fuselage (presumably next to the wing roots).

The vertical tail is evidently located between the two slipstreams. In the cruising condition (flaps neutral) the C^(6) function is fairly regular between plus and minus

RUDDER ANGLE REQUIRED FOR TRIM

20

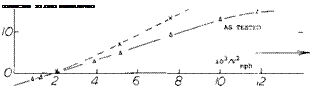
Pair of Slipstreams. The direction of propeller rotation in twin-engine airplanes will influence the flow pattern at, and stabilizing effect of the horizontal tail surface (28) and Chapter XII. The effect of the propellers on the directional stability of a B-28 for the case of both pro­pellers turning right are given on figure 40. The results for the flaps done case Tc = 1.3, C L = 2.0 are:

a) At /6 = 0 no tail, a moment is obtained corresponding to Qyi = — 0.01, turning the airplane to the left. The left slipstream seems to blow slightly across the fuse­lage.

b) The moment under (a) is doubled when adding the tail surfaces. A sidewash to the right, is evidently pro­duced at the location of the vertical tail by propeller blades and slipstream turning in this direction.

c) As in figure 28, the CT($) function is asymmetric. The stable range is wider when yawing to the right (to 5 – – 20°) and limited (to/5 = + 10°) when turning to the left (as seen by the pilot).

d) It seems, when turning to the left, the vertical tail begins to “lean” against the right-side slipstream at angles above /3 = + 20°. The slope increases to a maximum in the order of dC^/d/S = + 0.03.

e) When turning to the right, the tail surface seems to stall at an angle ft = — 20 or — 25°. The slope reverses to maximum values of dC^/dfi between — 0.03 and — 0.04.

n.

NORTH	AMERICAN	[ P-	51 "MUSTANG"
POSSIBLY THE FIRST OPERATIONAL
AIRPLANE USING A	LAMINAR-TYPE
FOIL	SECTION,	PRESUMABLY OF THE
64 SERIES WITH 16	to 11% THICK-
NESS	AND 1.2%	CAMBER DEVELOPED
AROUND 1942
b	37	ft	0.5 TAPERED
S	236	ft2	A = 5.8
d	10.5	ft	3-BLADED
Sv =	8.5%	S	RUDDER 52%
w	8000	lb	LOW WING

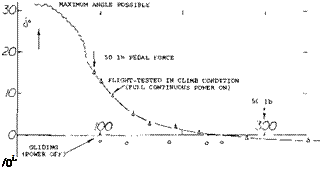
Figure 40. Rudder angles required to trim P-51 “Mustang”, flight- tested by NACA (31,c).

Opposite-Rotation (28). When arranging engines or pro­pellers, turning in opposite directions, flow pattern and directional characteristics evidently become symmetrical. Characteristics in figure 39 are as follows:

a) When yawing to the right, stalling takes place as in (e) above, in the case where both engines turn so that the blades sweep down at the inboard sides of the nacelles. Note that the left propeller turns clockwise (as in (e) above).

b) When yawing to the left, the same stabilizing inter­ference as in (d) above is obtained, in the case where the propellers turn sweeping up at the inboard sides. Note that the right propeller turns as in (d) above.

c) It is apparent that none of the three modes of twin – propeller rotation will remedy all of the irregularities in the yaw moment function. For displacement up to plus-minus 20°, contra-rotation as in (a) seems to be best, while at angles up to plus-minus 40°, the oppo­site mode of operation (blades up) is superior (at least in the B-28 configuration).

Shape, dimensions, arrangement, power used and other parameters may affect the directional characteristics of any specific airplane. However, the evaluation presented above, displays the type of interference to be expected between the vertical tail and the pair of slipstreams in twin-engine airplane configurations.