Inviscid Stability Theory and the Point-of-Inflection Criterion

Inviscid stability theory gives insight into instability mechanisms with the point-of-inflection criterion, which follows from the Rayleigh equation. It says basically, [15, 24], that the presence of a point of inflection is a sufficient condition for the existence of amplified disturbances with a phase speed 0 й cr й ue. In other words, the considered boundary-layer profile u(y) is unstable, if it has a point of inflection:[129]

d? u

v=° (8Л9)

lying in the boundary layer at yip

0 <yip й S. (8.20)

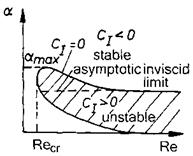
The stability chart of a boundary layer with a point-of-inflection of u(y) deviates in a typical way from that without a point of inflection. We show such a stability chart in Fig. 8.3.

For small Re the domain of instability has the same form as for a boundary layer without point of inflection, Fig. 8.2. This is the viscous instability part of the chart. For large Re its upper boundary reaches an asymptotic inviscid

Fig. 8.3. Schematic of a temporal stability chart of a boundary-layer with inviscid instability (ci = Ci) [27].

limit at finite wave number a. For large Re the boundary layer thus remains unstable.

When does a boundary-layer profile have a point of inflection? We re­member Fig. 7.4 and Table 7.1 in Sub-Section 7.1.5. There the results of the discussion of the generalized wall-compatibility conditions, eqs. (7.53) and (7.54), are given. We treat here only the two-dimensional case, and recall that a point of inflection exists away from the surface at ypoi > 0, if the second derivative of u(y) at the wall is positive: d2u/dy2w > 0. In a Blasius boundary layer, the point of inflection lies at y = 0.

With the help of Table 7.1 we find:

— A boundary layer is destabilized by an adverse pressure gradient (dp/dx > 0), by heating,[130] i. e., a heat flux from the surface into the boundary layer (dTw/dygw < 0) and by blowing (normal injection [28]) through the surface (vw > 0).

The destabilization by an adverse pressure gradient is the classical interpre­tation of the point-of-inflection instability. Regarding turbulent boundary layers on bodies of finite length and thickness, it can be viewed in the following way: downstream of the location of the largest thickness of the body we have dp/dx > 0, hence a tendency of separation of the laminar boundary layer. Point-of-inflection instability signals the boundary layer to become turbulent, i. e., to begin the lateral transport of momentum (in general also of energy and mass, the latter in gas mixtures in chemical non-equilibrium) by turbulence fluctuations towards the body surface.

The ensuing time-averaged turbulent boundary-layer profile is fuller than the laminar one, Fig. 7.5, which reduces the tendency of separation.[131]

Although the skin-friction drag increases, the total drag remains small, because the pressure or form drag remains small. The flat-plate boundary layer is a special case, where this does not apply.

If an adverse pressure gradient is too strong, the ordinary transition sequence will not happen. Instead the (unstable) boundary layer separates and forms a usually very small and flat separation bubble. At the end of the bubble the flow re-attaches then turbulent (separation-bubble transition, see, e. g., [15] and [29] with further references).

— An air boundary layer is stabilized by a favorable pressure gradient (dp/dx < 0), by cooling, i. e., a heat flux from the boundary layer into the surface (dTw/dygw > 0) and by suction through the surface vw < 0.

These results basically hold also for hypersonic boundary layers. Stability theory there deals with a generalized point of inflection [30]:

and with even more generalized (doubly generalized) forms, which take into account the metric properties of the body surface, see, e. g., [31].

A sufficient condition for the existence of unstable disturbances is the presence of the point of inflection at ys > yo. Here y0 is the point at which

Further it is required that the “relative Mach number” [25]

c

Mrel = M – – (8.23)

a

is subsonic throughout the boundary layer. In fact, the condition is МГе1 < 1. Here M is the local Mach number (M = u/a), c is the phase velocity of the respective disturbance wave which is constant across the boundary layer (c = c(y)), and a = a(y) is the local speed of sound.

The physical interpretation of the generalized point of inflection is [30]:

— (тілі) > 0: energy is transferred from the mean flow to the disturbance, the boundary-layer flow is unstable (sufficient condition),

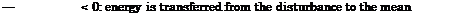d ( _1_ du ‘

dy T dy /

flow, the boundary-layer flow is stable,

~§y (т^у) = 0- no energy is transferred between disturbance and mean flow, the boundary-layer flow is neutrally stable.

A systematic connection of the generalized point of inflection to the sur­face flow parameters, as we established above for incompressible flow, is pos­sible in principle, but not attempted here. Important is the observation that
the distribution of the relative Mach number Mrel(y) depends also on the wall temperature. The thermal state of the surface is an important parame­ter regarding stability or instability of a compressible boundary layer.