Local and Material Rates of Change

The rate of change of properties measured by probes at fixed locations are referred to as local rates of change, and the rate of change of properties experienced by a material particle is termed the material or substantive rates of change.

The local rate of change of a property r is denoted by dr(x, t)/dt, where it is understood that x is held constant. The material rate of change of property r shall be denoted by Dr/Dt. If r is the velocity V, then DV/Dt is the rate of change of velocity for a fluid particle and thus is the acceleration that the fluid particle experiences. On the other hand, dV/dt is just a local rate of change of velocity recorded by a stationary probe. In other words, DV/Dt is the particle or material acceleration and dV/dt is the local acceleration.

For a fluid flowing with a uniform velocity Vx, it is possible to write the relation between the local and material rates of change of property r as:

dr Dr dr dt = Dt – a?

Thus, the local rate of change of r is due to the following two effects:

1. Due to the change of property of each particle with time.

2. Due to the combined effect of the spatial gradient of that property and the motion of the fluid.

When a spatial gradient exists, the fluid motion brings different particles with different values of r to the probe, thereby modifying the rate of change sensed by the probe. This effect is termed convection effect. Therefore, Vx (dr/dx) is referred to as the convective rate of change of r. Even though Equation (2.17) has been obtained with uniform velocity Vx, note that in the limit St ^ 0 it is only the local velocity V which enters into the analysis and Equation (2.17) becomes:

dr Dr dr

dt Dt dx

Equation (2.18) can be generalized for a three-dimensional space as:

where V is the gradient operator (= id/dx + jd/dy + kd/dz) and (V ■ V) is a scalar product (= Vx d/dx + Vy d/dy + Vz d/dz). Equation (2.19) is usually written as:

(2.20)

when n is the velocity of a fluid particle, DV/Dt gives acceleration of the fluid particle and the resultant equation is:

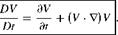(2.21)

Equation (2.21) is known as Euler’s acceleration formula.

Note that the Euler’s acceleration formula is essentially the link between the Lagrangian and Eulerian descriptions of fluid flow.