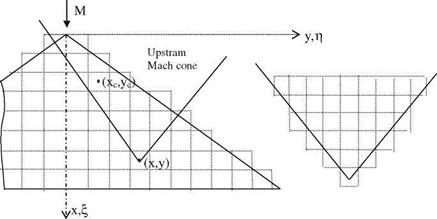
Mach Box Method

Mach Box Method is based on subdivision of the surface of the thin wing in a supersonic flow into small square boxes and summing the effect of all these boxes, as shown in Fig. 5.16, if all the edges of the wing are supersonic (Landahl and

Fig. 5.16 Mach Boxes on a delta wing and its Mach cone

Stark). In addition, if there are subsonic edges present using the concept of dia­phragm, it can be applied to more general cases. First, as shown in Fig. 5.16, let us see its application on a delta wing with all supersonic edges. The boxes in the upstream Mach cone of point (x, y) have influence on the point (x, y) being the center of any square box on the wing surface. Let the jth box with the center coordinates (xc, yc) on wing has its vertical displacement as hj, pitch angle a,-, and roll angle 0j. The total displacement effect of the jth box on any point (x, y) reads as

Zj(x, y, t) = ~[hj{xc, Ус) + (x – xc)aj(xc, yc) + (y – yj)0j(xc, yc)]eixt

The boundary condition at the surface becomes

w(x, y, t) = — i<nhj + ia>(x — xc)aj + ix(y — yj)0j + Uaj]eixt. (5.87)

Choosing the equally sized boxes small enough, the downwash for the jth box reads as

Wj = —(tXhj + Uaj)eixt = Wjeixt (5.88)

The amplitude of the lifting pressure coefficient was given in Eq. 5.86 in terms of downwash. If we sum the effect of all boxes influencing any point (x*, y*) on the wing surface the lifting pressure coefficient in summation notation reads as

Equation 5.89 is an expression with all complex elements. If it is written for all the boxes on the wing surface it will result in the following complex matrix equation.

К } =-4[R + ilfw} (5.90 — a)

p

Here, the complex matrix [Rj + ij is the pressure influence coefficient matrix whose elements are the induced velocity at a point (x*, y*) of box Vj.

V

The elements of this complex matrix depend only on the reduced frequency and the Mach number. Once the matrix is composed it can be used for all wing geometry which has supersonic edges. The lifting pressure coefficient at any point (x*, y*) on the surface can be evaluated without inversion of any matrix, i. e. explicitly as follows

While we are developing the Mach box technique we assumed that the lower and the upper surfaces of the wing do not interact with each other. This assumption

holds if all edges of the wing is supersonic, since only for the supersonic edges no information can be carried from one surface to another. The picture, on the other hand, is different for the subsonic edges. The surface between the outside of the leading edge of a subsonic edge and the Mach cone is called the diaphragm surface, Fig. 5.17.

On the surface of diaphragm there is downwash with unknown value wd, but there is no lifting pressure. This gives us the opportunity of partitioning Eq. 5.90 as follows (Hassig et al. 1969).

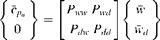(5.91)

Here,

Pww: Influence coefficient matrix of the wing on itself, square matrix Pwd- Influence coefficient matrix of the diaphragm on the wing,

PdW Influence coefficient matrix of the wing on the diaphragm,

Pdd’- Influence coefficient matrix of the diaphragm on itself, square matrix.

We can solve for the downwash value of the diaphragm using the second line of Eq. 5.91 as follows.

fWd } = -[Pdd ] 1[Pdw]{w }

and substituting the result in 5.91 gives us the desired lifting pressure coefficient.

{Cpa } = ([Pww] – [Pwd ][Pdd ] 1[Pdw^{W}

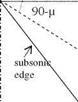
Fig. 5.17 Subsonic edge and the diaphragm

> y

x у

We have mentioned before that there is another method for solving the supersonic flow past thin wings. That was ‘Supersonic Kernel Function Method’. We are going to study that method next.