Mach wave reflection

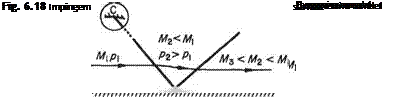In certain situations a Mach wave, generated somewhere upstream, may impinge on a sohd surface. In such a case, unless the surface is bent at the point of contact, the wave is reflected as a wave of the same sign but at some other angle that depends on the geometry of the system. Figure 6.18 shows two wavelets, one expansive and the other compressive, each of which, being generated somewhere upstream, strikes a plane wall at P along which the supersonic stream flows, at the Mach angle

appropriate to the upstream flow. Behind the wave the flow is deflected away from the wave (and wall) in the expansive case and towards the wave (and wall) in the compressive case, with appropriate increase and decrease respectively in the Mach number of the flow.

The physical requirement of the reflected wave is contributed by the wall downstream of the point P that demands the flow leaving the reflected wave parallel to the wall. For this to be so, the reflected wave must turn the flow away from itself in the former case, expanding it further to М3 > My, and towards itself in the compressive case, thus additionally compressing and retarding its down­stream flow.

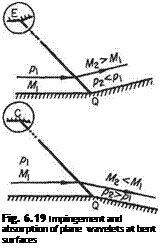
If the wall is bent in the appropriate sense at the point of impingement at an angle of sufficient magnitude for the exit flow from the impinging wave to be parallel to the wall, then the wave is absorbed and no reflection takes place, Fig. 6.19. Should the wall be bent beyond this requirement a wavelet of the opposite sign is generated.

A particular case arises in the impingement of a compressive wave on a wall if the upstream Mach number is not high enough to support a supersonic flow after the two compressions through the impinging wave and its reflection. In this case the impinging wave bends to meet the surface normally and the reflected wave forks from the incident wave above the normal part away from the wall, Fig. 6.20. The resulting wave system is Y-shaped.

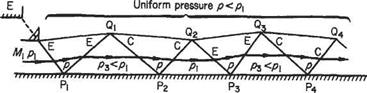
On reflection from an open boundary the impinging wavelets change their sign as a consequence of the physical requirement of pressure equality with the free atmo­sphere through which the supersonic jet is flowing. A sequence of wave reflections is shown in Fig. 6.21 in which an adjacent solid wall serves to reflect the wavelets onto the jet boundary. As in a previous case, an expansive wavelet arrives from upstream and is reflected from the point of impingement Pi while the flow behind it is expanded to the ambient pressure p and deflected away from the wall. Behind the reflected wave from Pi the flow is further expanded to ps in the fashion discussed above, to bring the streamlines back parallel to the wall.

On the reflection from the free boundary in Qi the expansive wavelet P1Q1 is required to compress the flow from p-у back to p again along Q1P2. This compression

Expansive wavelet

Compressive wavelet

Fig. 6.20

deflects the flow towards the wall where the compressive reflected wave from the wall (P2Q2) is required to bring the flow back parallel to the wall and in so doing increases its pressure to pi (greater than p). The requirement of the reflection of P2Q2 in the open boundary is thus expansive wavelet Q2P3 which brings the pressure back to the ambient value p again. And so the cycle repeats itself.

The solid wall may be replaced by the axial streamline of a (two-dimensional) supersonic jet issuing into gas at a uniformly (slightly) lower pressure. If the ambient pressure were (slightly) greater than that in the jet, the system would commence with a compressive wave and continue as above (Q1P2) onwards.

In the complete jet the diamonds are seen to be regions where the pressure is alternately higher or lower than the ambient pressure but the streamlines are axial, whereas when they are outside the diamonds, in the region of pressure equahty with the boundary, the streamlines are alternately divergent or convergent.

The simple model discussed here is considerably different from that of the flow in a real jet, mainly on account of jet entrainment of the ambient fluid which affects the reflections from the open boundary, and for a finite pressure difference between the jet and ambient conditions the expansive waves are systems of fans and the compressive waves are shock waves.