Outline of Stability Theory

We sketch now some features of linear stability theory. This will give us insight into the basic dependencies of instability but also of transition phenomena [15, 23, 24]. Of course, linear stability theory does not explain all of the many phenomena of regular transition which can be observed. It seems, however, that at a sufficiently low external disturbance level linear instability is the primary cause of regular transition [12, 18].

For the sake of simplicity we consider only the two-dimensional incom­pressible flat-plate case (Tollmien-Schlichting instability) with due detours to our topic, instability and transition in high-speed attached viscous flow. The basic approach and many of the formulations, e. g., concerning temporally and spatially amplified disturbances, however are the same for both incom­pressible and compressible flow [25, 26]. Our notation is that given in Fig. 4.1.

Tollmien-Schlichting theory begins with the introduction of split flow pa­rameters q = q + q’ into the Navier-Stokes equations and their linearization (q denotes mean flow, and q’ disturbance flow parameters). It follows the as­sumption of parallel boundary-layer mean flow, i. e., v = 0.[125] The consequence is du/dx = 0. Hence in this theory only a mean flow u(y) is considered, with­out dependence on x. Therefore we speak about linear and local stability theory. The latter means that only locally, i. e., in locations x on the surface under consideration, which can be chosen arbitrarily, stability properties of the boundary layer are investigated.[126]

The disturbances q’ are then formulated as sinusoidal disturbances:

q'(x, y,t) = q’A (y)ei(ax-uf). (8.3)

Here qA (y) is the complex disturbance amplitude as function of y, and a and ш are parameters regarding the disturbance behavior in space and time. The complex wave number a is with і = %/—1

a — ar + iai,

with

2n

ar T J ^x

Xx being the length of the disturbance wave propagating in x-direction. The complex circular frequency ш reads

ш — шг + іші, (8.6)

with

шг — 2nf, (8.7)

f being the frequency of the wave.

The complex phase velocity is

c = cr + ісі = (8-8)

a

Temporal amplification of an amplitude A is found, with a real-valued, by

1 dA d

Alt=M(lnA)=U,‘ = a’’C‘- (8’9)

and spatial amplification by

1 dA d

я*г-г(М4>—(8Л0)

with ш real-valued.

We see that a disturbance is amplified, if ші > 0, or ai < 0. It is damped, if ші < 0, or ai > 0, and neutral, if ші — 0, or ai — 0.

The total amplification rate in the case of temporal amplification follows from eq. (8.9) with

and in the case of spatial amplification from eq. (8.10) with

A(-T) = ei:0(-^)dx

Ao

If we assume ші or —ai to be constant in the respective integration inter­vals, we observe for the amplified cases from these equations the unlimited exponential growth of the amplitude A which is typical for linear stability theory with

and

respectively.

With the introduction of a disturbance stream function Ф'(x, y,t), where Ф(у) is the complex amplitude:

Ф’ (x, y,t) = Ф(у)еі(ах-Wt) (8.15)

into the linearized and parallelized Navier-Stokes equations finally the Orr – Sommerfeld equation is found:[127]

-^-(фуууу-ОаЧуу+аЧ). (8.16)

The properties of the mean flow, i. e., the tangential boundary-layer ve­locity profile, appear as u(y) and its second derivative uyy(y) = d2u/dy2(y). The Reynolds number Res on the right-hand side is defined locally with boundary-layer edge data and the boundary-layer thickness A[128]

Reg = (8.17)

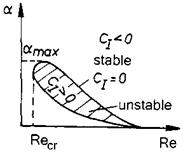
Obviously stability or instability of a boundary layer depend locally on the mean-flow properties u(y), uyy(y), and the Reynolds number Res. A typical stability chart is sketched in Fig. 8.2. The boundary layer is temporally unstable in the hatched area (ci > 0, see eq. (8.9)) for 0 < a A amax and Re A Recr, Recr being the critical Reynolds number. For Re ^ Recr we see that the domain of instability shrinks asymptotically to zero, the boundary layer becomes stable again.

For large Res the right-hand side of eq.(8.16) can be neglected which leads to the Rayleigh equation

(u — с)(Фуу — a2 Ф) — у, ууФ = 0. (8.18)

Fig. 8.2. Schematic of a temporal stability chart of a boundary layer at a flat plate (ci = a) [27].

Stability theory based on this equation is called “inviscid” stability theory. This sometimes is wrongly understood. Of course, only the viscous terms in the Orr-Sommerfeld equation are neglected, but stability properties of viscous flow can properly be investigated with it, except, of course, for the plain classical incompressible flat-plate flow.