PHUGOID MODE

Lanchester’s (ref. 1.1) original solution for the phugoid used the assumptions that Да = 0 and T — D = 0. It follows that there is no net aerodynamic force tangent to the flight path, and hence no work done on the vehicle except by gravity. The motion is then one of constant total energy, as suggested previously. This simplification makes it possible to treat the most general case with large disturbances in speed and flight-path angle (see Miele, ref. 1.7, p. 271 et seq.). Here we content ourselves with a treatment of only the corresponding small-disturbance ease, for comparison with the exact numerical result given earlier. The energy condition is

E = m, V2 — mgzB — const

or V2 = V2 + 2 gzE (9.2,1)

where the origin of FE is so chosen that V = Ve when zE — 0. With а. constant, and in addition neglecting the effect of q on CL, then CL is constant at the value for steady horizontal flight, i. e. CL = CL — Cw, and L = CweipV2>S or, in view of (9.2,1),

L = CWeip V2S + (CWepgS)zE =W+kzE (9.2,2)

Thus the lift is seen to vary linearly with the height in such a manner as
always to drive the vehicle back to its reference height, the “spring constant” being

* = CWJPgS (9.2,3)

The equation of motion in the vertical direction is clearly, when T — D — 0,

W — L cos в = mz,

On combining (9.2,2) and (9.2,4) we get

mzE + kzE = 0

which identifies a simple harmonic motion of period

T = 2w /— = 2tt

& V Gw. P9^

Since Gw = mg/lpVe2S, this becomes

T = чгл/2-

a beautifully simple result, suggesting that the phugoid period depends only on the speed of flight, and not at all on the airplane or the altitude! For the above example, Ve — 733 fps, and (9.2,5) gives T = 101 sec, a value 12.2 % different from the correct result, 115 sec.

Although (9.2,5) is a very useful result for the period, the above theory cannot give any information at all about the damping, since thrust and drag were eliminated from consideration and it is precisely these that cause the amplitude of the oscillation to change. For a better approximation, we return to the equations of motion and incorporate a simplification suggested by Fig. 9.2», i. e. Да = 0. Note that this is one of Lanchester’s two assumptions. If we drop one variable, we must also drop one equation of motion. Now the zero Да may be considered to imply zero pitching moment of inertia, so that pitch equilibrium is always maintained throughout the motion, and this suggests that it is the pitching moment equation that should be dropped. With Да and the Cm equation missing, (9.1,1) reduces to

(9.2,6)

For consistency with the previous numerical example, we neglect as well the derivatives CLp, CDp, CLq, CL^. Now the second of the three equations is an algebraic relation, i. e. with the preceding approximations

332 Dynamics of atmospheric flight The “undamped” period is seen to be

GWe ‘ PS(cl2) ‘ 2Ve

After eliminating GWc this reduces exactly to (9.2,5) so that the Lanchester result is recovered from (9.2,9) when CTy = 0.

For the case of horizontal flight under consideration here, GTp depends only on the reference drag coefficient and the type of propulsion system (see Sec. 7.8). For the example airplane in horizontal flight CTp —2GD, and in that case the damping coefficient is

To this approximation, £ will always vary inversely as the (L/D) ratio, but for constant-power propulsion (instead of constant thrust) the constant is 3/2V2 (instead of 1/V2).

The accuracy of the approximation given by (9.2,9) is illustrated on Figs. 9.4a, 9.8, and 9.16.

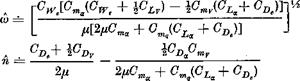Another approximation that gives better results for the period, but not necessarily for the damping, is one originally due to Bairstow (ref. 1.4) [the derivation is given by Ashkenas and McRuer (ref. 9.5)]. When converted to the notation of this work, it gives