Pitot tube equation

The pressure registered by a small open-ended tube facing a supersonic stream is effectively the ‘exit’ (from the shock) total pressure />02, since the bow shock wave may be considered normal to the axial streamline, terminating in the stagnation region of the tube. That is, the axial flow into the tube is assumed to be brought to rest at pressure />02 from the subsonic flow p2 behind the wave, after it has been compressed from the supersonic region p ahead of the wave, Fig. 6.10. In some applications this pressure is referred to as the static pressure of the free or undis­turbed supersonic stream p and evaluated in terms of the free stream Mach number, hence providing a method of determining the undisturbed Mach number, as follows.

From the normal shock static-pressure ratio equation (6.43)

/>2 _ 27M – (7 ~ 1)

P 7+1

From isentropic flow relations,

/>02 P2

Pea. I

M p p щ

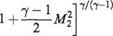
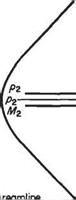
Dividing these expressions and recalling Eqn (6.49), as follows:

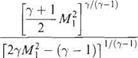(6.57)

This equation is sometimes called Rayleigh’s supersonic Pitot tube equation.

The observed curvature of the detached shock wave on supersonic Pitot tubes was once thought to be sufficient to bring the assumption of plane-wave theory into question, but the agreement with theory reached in the experimental work was well within the accuracy expected of that type of test and was held to support the assumption of a normal shock ahead of the wave.[29]