Plane oblique shock relations

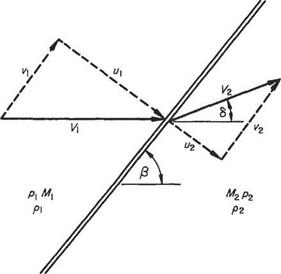
Let a datum be fixed relative to the shock wave and angular displacements measured from the free-stream direction. Then the model for general oblique flow through a plane shock wave may be taken, with the notation shown in Fig. 6.23, where V is the incident flow and V2 the exit flow from the shock wave. The shock is inclined at an angle /3 to the direction of Vi having components normal and tangential to the wave front of щ and vi respectively. The exit velocity V2 (normal м2, tangential V2 components) will also be inclined to the wave but at some angle other than /3. Relative to the incident flow direction the exit flow is deflected through 6. The equation of continuity for flow normal to the shock gives

pm = P2U2 (6.70)

Conservation of linear momentum parallel to the wave front yields

pmvi = P2U2V2 (6.71)

i. e. since no tangential force is experienced along the wave front, the product of the mass entering the wave per unit second and its tangential velocity at entry must equal

Fig. 6.23

the product of the mass per second leaving the wave and the exit tangential velocity. From continuity, Eqn (6.71) yields

(6.72)

Thus the velocity component along the wave front is unaltered by the wave and the model reduces to that of the one-dimensional flow problem (cf. Section 6.4.1) on which is superimposed a uniform velocity parallel to the wave front.

Now the normal component of velocity decreases abruptly in magnitude through the shock, and a consequence of the constant tangential component is that the exit flow direction, as well as magnitude, changes from that of the incident flow, and the change in the direction is towards the shock front. From this it emerges that the oblique shock is a mechanism for turning the flow inwards as well as compressing it. In the expansive mechanism for turning a supersonic flow (Section 6.6) the angle of inclination to the wave increases.

Since the tangential flow component is unaffected by the wave, the wave properties may be obtained from the one-dimensional flow case but need to be referred to datum conditions and direction are different from the normal velocities and direc­tions. In the present case:

or

(6.73)

Similarly

(6.74)

The results of Section 6.4.2 may now be used directly, but with M replaced by M sin /3, and М2 by М2 sin (/3 — S). The following ratios pertain:

Static pressure jump from Eqn (6.43):

p2 _ (7+ l)Mf sin2/9

pi 2 + (7 – 1 )M sin2 /3

or from Eqn (6.46)

p_ (7 + 1 )M sin2(/? – 6)

Pi 2 + (7 — )M% sin2(/3 — 6)

Static temperature change from Eqn (6.47):

Tj _ 27M sin2 /3 — (7 — 1) 2 + (7 — 1 )M sin2 /3 T 7+1 (7 + )M] sin2/3

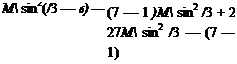Mach number change from Eqn (6.49):

The equations above contain one or both of the additional parameters /3 and (5 that must be known for the appropriate ratios to be evaluated.

An expression relating the incident Mach number M, the wave angle /3 and flow deflection 8 may be obtained by introducing the geometrical configuration of the flow components, i. e.

— = tan/3, — = tan(/3 — 8) Vi v2

but

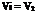and ^ = K M2 Pi

by continuity. Thus

Equations (6.77) and (6.81) give the different expressions for pi/pi, therefore the right-hand sides may be set equal, to give:

tan /3 _ (7 + 1 )M sin2 /3

tan(/3 – 8) ~ 2 + (7 – 1 )M sin2 /3

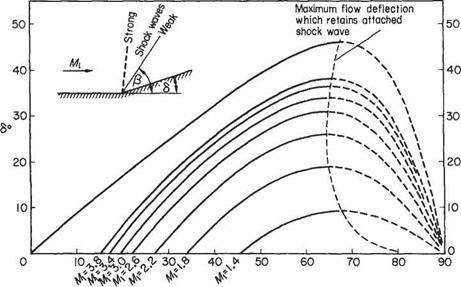
Plotting values of /3 against 8 for various Mach numbers gives the carpet of graphs shown in Fig. 6.24.

It can be seen that all the curves are confined within the M1 = 00 curve, and that for a given Mach number a certain value of deflection angle 8 up to a maximum value 8m may result in a smaller (weak) or larger (strong) wave angle /3. To solve Eqn (6.83) algebraically, i. e. to find /3 for a given M1 and 8, is very difficult. However, Collar* has shown that the equation may be expressed as the cubic

x3 – Cx2 — Ax + (B — AC) = 0

* A. R. Collar, JRAeS, Nov 1959.

Fig. 6.24

/3°

where

x = cot Д A = M2 — 1, В = ^ ^ * М tan 5

and

C= + tan<5

He further showed that the first root may be obtained from the iterative process

and a suitable first approximation is x

The iteration completed yields the root xq = cot Ду where Ду is the wave angle corresponding to the weak wave, i. e. Ду is the smaller value of wave angle shown graphically above (Fig. 6.24). Extracting this root (xo) as a factor from the cubic equation (6.84) gives the quadratic equation

x2 + (C + x0)x + [x0(C + xq) — A] — 0 having the formal solution

Now xo — cot/3w is one of the positive roots of the cubic equations and one of the physically possible solutions. The other physical solution, corresponding to the strong shock wave, is given by the positive root of the quadratic equation (6.87).

It is thus possible to obtain both physically possible values of the wave angle providing the deflection angle S < <5max may be found in the normal way by differentiating Eqn (6.83) with reference to /3, with M constant and equating to zero. This gives, for the maximum value of tan 6:

Substituting back in Eqn (6.82) gives a value for tan<5n