Pressure Uncertainty of Lifetime-Based Methods

7.4.1. Phase Method

The phase method for PSP measurements, as described in Chapter 6, determines pressure by

where tan (p = ojt = – Vc/Vs is uniquely related to the lifetime for a fixed modulation frequency, and Vc =-Am %HMf sin(f) and Vs = Am %HMeffcos(p) are

the DC components from the low-pass filters. The error propagation equation gives the relative variance of pressure

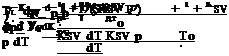The first term is the uncertainty related to temperature, the second is the uncertainty in PSP calibration, the third is the error in the given reference lifetime, and the last two terms are the uncertainties associated with the measurement system composed of a photodetector and lock-in amplifier. The sensitivity coefficients in Eq. (7.14) are

e Vc д p c

SVc = – — = SV

Compared to the intensity-based method discussed in Chapter 4, many error sources associated with model deformation do not exist, which reflects the advantage of the lifetime-based method. When the photon shot noise of the detector dominates, the pressure uncertainty is mainly contributed by the last two terms in Eq. (7.14). In the photon-shot-noise-limited case, the uncertainties in the outputs of the detector and lock-in amplifier are var(Vs) = ^^GhvBd and

The estimate Eq. (7.15) for the phase method is similar to Eq. (7.4) for the intensity-based CCD camera system. The behavior of the pressure uncertainty as a function of pressure and the Stern-Volmer coefficient B is similar to that shown in Figs. 7.4 and 7.5.

S,0 ——= 1 + 1/(KsvP) , 0 P d Г0

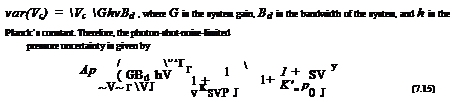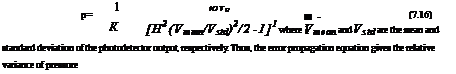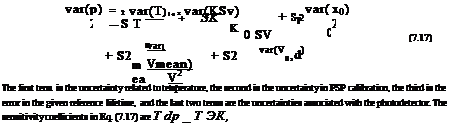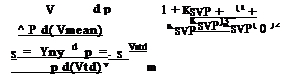In the photon-shot-noise-limited case, the uncertainties in the detector outputs

are Var(Vmean ) = VmeanG hv Bd and var(Vtd ) = Vstd Ghv Bd. Thus the photon-shot-

noise-limited pressure uncertainty is

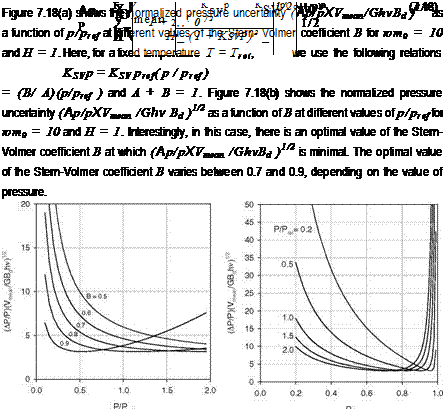
Fig. 7.18. The normalized pressure uncertainty (Ap/p)(Vmean/GhvBd )1/2 in the amplitude demodulation method with ют0 = 10 and H = 1 as a function of p/pref for different values of the Stern-Volmer coefficient B, and a function of B for different values of p/pref