Remarks on Lift and Drag of a Finite Wing from Lifting-Line Theory

It is now useful to summarize and focus on important features of the lifting-line theory.

1. Lift-Curve Slope

Recall from Eq. 5.74 that the two-dimensional lift coefficient is given by:

C, = m0(« -«L0) = m0aa,

where aa is the absolute angle of attack. Because the angle of zero lift of the section is a function of the airfoil shape and, hence, is independent of a, the two­dimensional lift-curve slope is given by:

dC,

——l = m0 per radian (two-dimensional) (6.50)

da 0

Recall that m0 = 2n from thin airfoil theory.

Recalling Eqs. 6.42, 6.45, and 6.46, which are valid for an untwisted finite wing of constant section with an elliptical-lift distribution and constant a;, we write:

Solving:

C = m0aa 1 + – ^

Again, the zero-lift angle is independent of the geometric angle of attack so that:

This is the lift-curve slope for a finite wing. Using the thin-airfoil theory result for m0,

dCT 2n

—L = m =——— .

da і + 2 ‘ (6.53)

+ ~AR

These results, which specify the lift-curve slope for a finite wing with elliptical loading, may be modified to describe a wing with arbitrary spanwise loading by inserting a correction factor, t. Thus,

The correction factor, t, depends on the values of the An’s in the Fourier series and has a typical value of 0.05 < t < 0.20.

The lift-curve slopes for a two-dimensional airfoil and a three-dimensional untwisted wing of constant section with elliptical loading and the same airfoil section are compared in Fig. 6.17. Notice that the finite-wing effect is to reduce the lift-curve slope of the wing compared to that for the airfoil sections that comprise the wing.

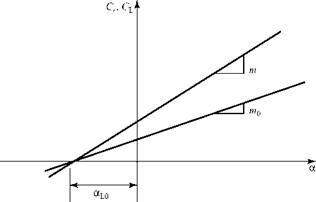When the airfoil lift coefficient is zero for a two-dimensional airfoil, Eq. 5.74, then a = aL0. For an untwisted wing of constant section with elliptical loading, Eq. 6.51 states that when CL = 0, then a = aL0 because a = 0. Because the airfoil and the wing in Fig. 6.17 have the same section, the intercept at Cl = CL = 0 is the same for both curves.