Solutions of Laminar Boundary Layer Equations at Hypersonic Speeds

Following Lees [131], Hayes and Probstein [1] and Cheng [132], the boundary layer equations are rewritten in terms of Howarth-Dorodnitsyn variables

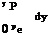
(12.205)

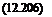
where Re = peuel/pe and p/p0 = cT/T0. Assuming Pr = 1, one obtains

where e = (y – 1)/(y + 1). f is a reduced streamfunction such that df /dn = u/ue and g = (H — Hw)/(He — Hw). h consists of terms including J0x pdx.

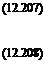The boundary conditions are

Therefore, for small e, there is a similar solution governed by Blasius equation and in this case, g = df/dg.

If terms of order є are retained, solutions for heat transfer rate, skin friction and displacement thickness can be written explicitly in terms of pressure distribution. The results of this analysis, called local similarity, are given in terms of a nondimensional parameter x which depends on M0 and Re (which is called the hypersonic viscous interaction parameter)

(12.209)

The Stanton number and skin friction coefficients based on the edge conditions

are i/2

M3 St ~ 0.332^ (12.210)

Cf ~ 2St (12.211)

Mo у ~ є ^0.664 + 1.73 T j x Ц* f-dxj (f j (12.212)

Notice that S* ~ S.

Hayes and Probstein [1] reviewed similar solutions of boundary layers with chemi­cal reactions including constant pressure solutions, stagnation point solutions, locally similar solutions with Pr = 1. Discussions of local similarity concepts can be found in [1] as well as in the work of Moore [133].

We will consider next the integral methods, where the profiles of the unknown functions are assumed and hence the partial differential equations are reduced to ordinary differential equations. The integrated momentum and energy equations give an estimate of the x-dependence of the boundary layer solutions and indicate when the local similarity concept breaks down.

Following Shapiro [129] and Schlichting [130], the integral momentum equation is given by

d Ґ t 2 2 d Г

— Peue – pu dy – щ— (peue – pu) dy = rw (12.213) or, in terms of displacement thickness S* and momentum thickness в, the above equation becomes

1 d S* due tw

Pe u2e) + – = – w (12.214)

ue dx

The integral energy equation is given by

or, in terms of the enthalpy thickness for He = const.

d 6 h qw

dx pe UgHg

To avoid assuming the profiles of unknown functions, numerical solutions of the boundary layer equations can be obtained using finite difference methods. Appli­cations to hypersonic flows, with and without chemical reactions are reported by Blottner [134].