Supersonic Flow About a Profile

In a supersonic flow any point in the flowfield is affected by the points lying inside of its upstream Mach cone. For this reason, unlike subsonic flow, even for a wing with infinitely long span we have to consider the three dimensional problem. This means, two dimensional analysis of a supersonic external flow cannot take into consideration the true physical behavior of a lifting surface while calculating its aerodynamic coefficients. However, for academic purposes, we are going to treat a wing section as a two dimensional flow case and obtain the lifting pressure coefficient for the sake of demonstrating the integrations involved in the process.

In a two dimensional flow the source strength remains constant in spanwise direction. For this reason the velocity potential 5.67 can be expressed as follows.

n1 p

/(x, z, 0=b A(n) (eixs1 + eixs2 )dh dn,

b 0 0 (5.68)

We can find the downwash expression by differentiating Eq. 5.68 with respect to z using the Leibnitz rule as follows.

П1 P P

= b A(n)J! Z(eixS1 + eixs2)d0dn + b0|а(П1) / (eixs1 + eixs2)dd

0 0 0

(5.69)

First term of right hand side of 5.69 as inner integral becomes

(eixs1 + eixs2) = ™ sin 0Og0(eixS1 _ eixs2) = sin e(eixT1 _ eixs2) (5.70)

The second term of 5.69, using the fact that, for П = П1, go = 0 and s1 = s2,

The relation 5.64 stated that depending on (x, y, z) being at the upper or lower surface of the wing we have (П1)и1 = x ^ b z.

By differentiation we obtain

We observe from 5.72 that the second integral of 5.69 is independent of в to give

?1 p

(дф = irnz _ eimi) s. n ^T 2 pA(n1)e,’“(tTiMbz) (5.73)

z u i ab2 Па

Taking the limits for 5.73 for lower and upper surfaces the downwash value becomes

Using 5.74 in 5.73 gives us the velocity potential value as follows

6

0

In order to integrate 5.75, the integrand of the inner integral must be function of в only. We can write the integrand as follows

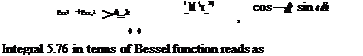p

p

J0(z) = ■ cos(z sin h)dh

p

0

and it gives us the velocity potential as

We need to express Eq. 5.77 in nondimensional form while obtaining the lifting pressure coefficient for a thin airfoil. Here, we use the following nondimensional quantities

n* = n/b, n* = n/b, k = b—/U, – = kM2/b2

This results in following expression for the velocity potential

We know the pressure coefficient in terms of the velocity potential. For a simple harmonic motion the amplitude of the pressure coefficient in terms of the velocity potential reads as

Since the difference between the lower upper surface pressures gives the lifting pressure if we use Eq. 5.78 without the thickness effect, the lifting pressure coefficient

frequency of 0.20 obtain the amplitude of lifting pressure coefficient for simple harmonically heaving airfoil with amplitude p*.

Solution: With the aid of Mathematica the real and the imaginary parts of Eq. 5.79 can be evaluated along the chord using numerical integration. The graphs of real and imaginary parts of the lifting pressure are plotted below.

Cpa Imaginery Part of Cpa

x

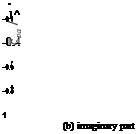0.2 0.4 0.6 0.8 1

The integral of the real and imaginary parts give the amplitude of the sectional lift coefficient in terms of the heave amplitude as follows.

Pei = (-0.055883 – 0.705385i)P*.