Supersonic Kernel Method

We have seen the kernel function method for subsonic flows. Now, we are going to use a similar approach to develop supersonic kernel method based on the accel­eration potential. The relation between the acceleration potential and the velocity potential for simple harmonic motion was

W = іюф + U фx

and its solution was

x
ф = 1 e-ixx/U j W(k, y, z)eixk/Udk

The acceleration potential was related to the lifting pressure and it was in the following form

W = A°eix[t-M(x-n)/ab2±R/ab2]/R, R =l(x – П)2 – b2[(y – g)2 + z2]

oz v

For the velocity potential we can write

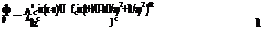x-n

0 –

Here, L(n, g) is the unknown lifting pressure at the wing surface. In supersonic flow, we know that the acceleration potential is affected by two different wave front to give the solution in following form

) cos(M—)

R

The supersonic kernel method is based on the numerical solution of a matrix system formed with finite number of points taken for the integral equation written above. It is applicable to the wing geometries having subsonic leading edges and supersonic trailing edges. The matrix system formed by the numerical integration is difficult to invert, however, with proper choice of pressure modes it becomes invertible (Cunningham 1966).