The Compressible Gust – Schwarzschild’s Technique

Compressible alternatives to von Karman & Sears’ theory have been proposed and reviewed for instance by Goldstein (1976). The approach proposed by Amiet (1976) is selected here for its formal simplicity and the wide possibilities of extensions it offers, discussed later on. In particular the solution will be easily extended in a three-dimensional context. At low frequencies it reduces to a compressibility correction of the incompressible theory, described in the references. The correction is not addressed here because it remains quite close to original Sears’ solution for compact airfoils. Of more interest is the case of non-compact airfoil chords and related high frequencies, for which the solution is detailed below.

Sears’ problem is considered now in a three-dimensional space, thus in­troducing oblique gusts. A gust is defined by two aerodynamic wavenumbers ki and k2 in the streamwise (chordwise) and spanwise directions respectively

X

Figure 5. Two-dimensional gust for generalized Sears’ problem statement.

by the upwash, w(k1,k2) e1 (kl X2+k2 X2-w t’) (Fig. 5). For convenience, the no­tation (y1,y2,y3) is devoted later on to the source point (with y3 = 0) and (x1, x2,x3) to the observation point or any field point. When evaluating the unsteady lift the airfoil is assumed of infinite span, as also featured in the figure, so that the potential is factorized as ф(х1,х2, t) ei (k2 Х2-ш b in accor­dance with the excitation by the gust. This leads to the modified convected Helmholtz equation, equivalent form of the linearized Euler and continuity equations

to be solved with the rigidity condition on the surface of the airfoil and a Kutta condition in the wake. This equation is reduced to the ordinary Helmholtz equation by a change of variables referred to as Ribner’s trans­formation:

where Graham’s parameter @ = M0 Щ_/(вЩ) has been introduced for con­venience. When @ is smaller than 1 the gust is said sub-critical and the
equation is elliptic. The disturbance potential attenuates as an evanescent wave away from the airfoil leading edge. When 0 is larger than 1 the gust is supercritical and the potential radiates to the far field as sound. This is why the interest is often limited to supercritical gusts as the only contributing ones in the sound field. But this is true only in the limit of infinite or arbi­trary large span and if the problem is addressed to directly derive the sound. In the following two-step approach the equation is solved first to derive the induced unsteady lift, which is the trace of the sound on the airfoil. The sound itself is calculated afterwards from its trace by taking into account the source distribution over the actual span, and this truncation makes the sub-critical gusts contribute as well. In other words the sources are evalu­ated ignoring the span-end effect. It is worth noting that sub-critical and supercritical gusts correspond to subsonic and supersonic phase speeds of their trace along the leading edge with respect to the incident mean flow, respectively, as pointed out by Amiet (1975).

The aeroacoustic response of the airfoil is now interpreted as a wave scattering problem. The approach is outlined as a reference that can be applied in many more complicated configurations. The focus is first on the induced lift and the acoustic field will be addressed in the next section, essentially because the complete mathematical problem has no analytical solution. Furthermore even the finite-chord strip representing the airfoil cannot be handled exactly from this standpoint. The solution proposed by Amiet (1976) is to consider separately the contributions of the leading edge and of the trailing edge within the scope of an iterative procedure called Schwarzschild’s technique (see Landahl (1961)). The theoretical background is Schwarzschild’s theorem, stated as follows. Let ф be a scalar field solution of the Helmholtz equation

with the boundary conditions:

ф(хі, 0) = F(xi) xi > 0,

This theorem is inherited from electromagnetism (the complex conjugate can need being taken depending on the choice of convention for the time Fourier transform). It produces closed-form solutions provided that the integral can be calculated analytically, which is always the case when dealing with gusts defined by complex exponentials.

Only the principle is explained here. For the application the airfoil is first assumed semi-infinite by removing the trailing edge to infinity downstream. A zero-order disturbance potential is introduced that exactly cancels the incident gust upwash not only on the airfoil surface but also everywhere on x3 = 0. This potential is balanced upstream of the leading-edge by a first-order contribution for which the transformed potential Фі is solution of a Schwarzschild’s problem. Indeed Ф1 is prescribed upstream of the leading edge and its normal derivative must be zero on the extended airfoil surface. Once determined, it is transformed back to get the effective potential ф1, and the pressure jump I = Ap1 = 2 p1 is deduced by the relationship in the presence of flow

This first iteration alone is wrong because the actual airfoil chord is not infinite. Therefore a trailing-edge correction is introduced, calculated as if now the leading edge was removed to infinity upstream. The difference is that the disturbance pressure is used to write down another Schwarzschild’s problem, because the Kutta condition states that this pressure must be zero in the wake and have a zero normal derivative on the airfoil surface (the details, not given here, again involve changes of variables to move the origin of coordinates from the leading edge to the trailing edge). In principle higher-order iterations could be performed but the first two are enough in practice, as pointed out by Amiet (1976). Details can be found in the referenced papers. In the present three-dimensional context, the full solution for the distributed unsteady lift of supercritical oblique gusts including main leading-edge impingement and trailing-edge back-scattering reads (Mish & Devenport (2000), Roger (2010))

introducing the non-dimensional chordwise coordinate yl with origin at the

center chord, and the notation к = p 1 — 1/02 = Jp2 — Щ 2/в2. E is the function introduced by Amiet and involving Fresnel integrals

eu

. dt. о л/2 nt

The same expression for the unsteady lift and more generally for Schwarz – schild’s eq. (4) or the complex conjugates are found in the literature de­pending on the definition of Fourier transforms; remind that in the present document time dependence is assumed as e-lut.

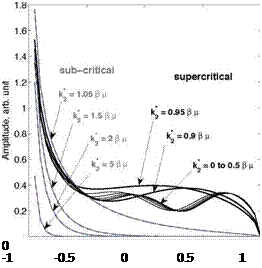
For sub-critical gusts к is replaced by i к’ with к’ = J(k|2/в2) — p2 and the term involving the function (1 — i) E by the error function erf ([2 к’ (1 — y’^)}1/2). All gusts involve the integrable inverse square-root singularity at the leading edge already pointed out by Sears’s solution, but the unsteady lift of sub-critical gusts decreases much faster farther downstream. This is emphasized in Fig. 6, where the chord-wise distribution of the unsteady lift amplitude on a flat-plate airfoil is plotted for various oblique gusts con­tributing to the same frequency, thus various angles triggered by different values of k2. Despite the physical drop at the trailing edge imposed by the Kutta condition, the lift induced by supercritical gusts contaminates more significantly the aft part of the airfoil.

Including sub-critical gusts in the modeling and paying attention to the sub – or supercritical duality of sinusoidal gusts is important for practical applications. Typically analytical studies of rotating blade broadband noise rely on a strip-theory approach: a blade is split into segments, each of which is assimilated to a rectangular airfoil of small aspect ratio, in order to account for span-wise varying conditions. If a two-dimensional response of each segment is assumed for simplicity, only parallel gusts are abusively selected, supercritical by definition. If the actual excitation by oncoming disturbances tends to produce sub-critical conditions, substantial errors are expected.

In its original two-dimensional declination for parallel gusts (k2 = 0) the compressible high-frequency solution holds whenever p = kc/(2в2) > n/4 or whenever c/в2 > A/4. Very low frequencies are possibly addressed by the technique but would a priori require a larger number of iterations, not compatible anymore with the derivation of closed-form solutions. Classical Sears’ solution could provide a good alternative for gust-impingement at a leading edge at low frequencies, used together with Graham’s similarity rules (see Graham (1970)). The mathematical limitation must be transposed to the parameter к instead of p in the general case, leading to possible concern for values of k2 approaching the transition between sub-critical and supercritical gusts. A palliative interpolation between both regimes can be

yi

Figure 6. Typical chord-wise distribution of unsteady lift amplitude for various oblique gusts in both sub-critical and supercritical ranges. kc = 2 n, M0 = 0.3.

applied instead as proposed by Roger & Moreau (2005) for the similar case encountered in trailing-edge noise modeling.