THE DESIGN OF CLASSICAL AND SWEPT AIRCRAFT

5.1 Some design aims for swept wings. It is not a straightforward matter to set oneself reasonable and worthwhile aims in the aerodynamic design of air­craft. He have already seen in Sections 1.4 and 4.1 that very many other as­pects, apart from aerodynamics, must be considered and that the final synthe­sis of all these inputs will determine the actual design. Also, many aerody­namic advances may, in the end, not be taken up as improvements in aerodynamic performance or handling but may be realised, at secondhand as it were, by im­provements in other respects, e. g. by allowing the use of wings of increased thickness or of lower sweep or of simpler construction, with their attendant advantages in structure weight, cost of manufacture, or maintenance; or by al­lowing greater safety margins or increased flexibility in operation; or by re­ducing the intensity and size of the noise footprint. Since none of these cross feeds and exchange rates have yet been investigated in any generality, we cannot specify the aerodynamic aims in any detail and we cannot assess their value with any accuracy, except in specific cases when thorough engineering design studies can be carried out. Such studies go beyond the scope of this book, and we must, therefore, concentrate here on more general design criteria and concepts.

In general terms, there is one aerodynamic aim which we have already seen many times to be indispensable and peremptory: to design for a well-ordered healthy type of flow under all flight conditions, which is calculable, measurable, and predictable (see E C Maskell (1961), J A Bagley (1961), D Ktichemann (1968)).

It will be clear from the discussion so far that even this general aim has not yet been reached: there are as yet no rational and complete design methods, and risks are taken in aircraft design, often at great expense in every sense, because some essential aerodynamic characteristic in flight cannot be calcula­ted or measured or predicted by any means. Therefore, we are concerned here once again not so much with describing well-established solutions but with de­fining problems that remain to be solved. However, we have at least progres­sed far enough to recognise real problems which, we think, should be soluble.

We have already seen that there is a fundamental conflict between the design aims for various flight conditions of swept-winged aircraft, and that one way out of this dilemma is to design different geometric configurations for seve­ral design points at different flight conditions, the different geometries or schemes being such that one can readily be transformed into another. For ex­ample, transport aircraft may be regarded as having at least three main design points: (1) climb-out at the take-off safety speed, with high-lift devices

extended in their take-off setting; (2) cruising flight, with a "clean" wing; and (3) landing, with high-lift devices extended in the appropriate landing setting. At each point, there are important off-design conditions to be con­sidered, such as the behaviour near and beyond the stall, in gusts, and near and beyond the buffet boundary. Also, there are important off-design condi­tions to be considered along the flight envelope linking these design points.

On our design experience so far, it is probably justified to state some furth­er general design aims and trends which cover all these cases: to load up sin­gle or multiple lifting surfaces as much as possible, with the least expense in energy and engineering complication, in a manner which ensures aerodynamic stability and control; to exploit to the full the three major sweep effects described in Section 4.2 and, in particular, to realise the suction forces along the leading edge, which are implied in this flow model; and to capture more and more air and to supply it with energy in one form or another, for the purpose of propulsion and possibly also of generating lift. The general aims will at least provide a basis for the subsequent discussion.

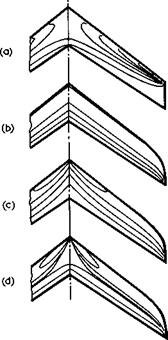
Fig. 5.1 Various isobar patterns on sweptback wings (schematic)

We shall find that design criteria for exploiting the sweep effects are the least well-defined. Although we have already noted how large the threedimen­sional tip and kink effects are and how they can be estimated, the major sweep effects have been derived in terms of sheared wings of infinite span and we must, therefore, consider how they may be realised and their benefits exploi­ted on a real wing of finite span. Useful indications and pointers may be ob­tained from isobar patterns on the upper surface of a typical, thick and lif­ting, sweptback wing, as sketched in Fig. 5.1. Case (a) represents an "un­treated" wing at low or high-subcritical speeds, with strong non-uniformities in the isobar pattern mainly due to centre and tip effects, as explained in Section 4.4 (see also Fig. 4.24). Such a threedimensional pattern is far away from that on an infinite sheared wing and the possible beneficial effects of sweep cannot be expected to be realised in full, whereas the undesirable fea­tures of a finite swept wing are all there: unnecessarily low critical Mach numbers owing to loss of isobar sweep, premature flow separation near the wing tips owing to unnecessarily high suction peaks and steep adverse pressure gra­dients with a consequent tendency of the wing to pitch up and make matters worse, etc. The flow over an untreated supercritical wing, as in Figs. 4.69

and 4.71, is even worse in the sense that it departs even further from the flow over the corresponding infinite sheared wing with a local supersonic re­gion. This demonstrates quite forcibly the need for "designing" swept wings.

These shortcomings were realised soon after the sweep effects were discovered and applied: they follow simply from the fact that the subcritical curved – streamline flow associated with infinite sheared wings (Fig. 4.6) is distur­bed in various ways. R Buschner (1944) was the first to realise this and to suggest that shapes should be modified in such a way as to pull the isobars straight at the full angle of sweep and to demonstrate that this is possible (see also D Ktlchemann (1947) and D KUchemann & J Weber (1953)). This leads to a simple and rather obvious general design criterion: it is beneficial to design swept wings to have straight and fully-swept isobars all along the span and right into the centre. This is illustrated in case (b) of Fig. 5.1 (in anticipation of the discussion in Section 5.3 below, a tip shape with a cur­ved leading edge is shown here, which may help to keep the isobars swept al­most up to the wing tip). However, straight isobars are evidently not a ne­cessary condition’, they would establish pressures as on an infinite sheared wing everywhere on the threedimensional wing but, as might be expected, on different shapes and it is not obvious that this would be fully effective, let alone the best that can be done. There is no reason to suppose that, for ex­ample, sweeping the isobars even more highly in the central region, as indi­cated in case (c) of Fig. 5.1, might not lead to better results. Thus the question of what isobar patterns to aim at, even in wholly subcritical flow, has not yet been answered.

Matters are even more uncertain when it comes to design criteria for supercri­tical wings. It is quite obvious that an untreated wing will not reap the be­nefits of sweep, as indicated in case (c) of Fig. 4.8 for a supercritical flow over an infinite sheared wing. It seems strange to have to record that not much serious attention has been given to the threedimensional design problem, possibly because of preoccupation with computing matters or twodimensional flows or with experimental problems. As long as the design criteria are not clarified, activities are proceeding rather in the dark without realistic en­gineering aims. Attempts to design wings to have fully-swept isobars and su­percritical lift from flows such as those in Fig. 4.58 only around mid-semi­span and to let the isobars close before they reach the central and tip re­gions and thus to unload these, simply avoid the crucial problem; they are not making the most effective use of the wing area and are not likely to lead to effective solutions. Ways must be found to load up the whole wing as uniform­ly as possible, within the limitations imposed by the physics of transonic flows, but we do not yet know in which direction to proceed. What can be said is wholly speculative, and the isobar pattern in case (d) of Fig.5.1 may, or may not, be realistic. This pattern would retain some of the features of the shockwave system of Fig. 4.69, but supplement it by incorporating some shock­less compressions and by building up lift near the apex of the wing in the manner of a conical flow. Some such type of flow is needed there because the flow is essentially threedimensional, and supercritical lift cannot be obtai­ned in the same manner as in the twodimensional flow of Fig. 4.58. Other pos­sible planform modifications near the apex of the wing will be discussed in Section 5.4.

Nevertheless, if any of the patterns (b), (c), or (d) in Fig. 5.1 could be re­alised in practice, then there would be a large region on the wing where shea – red-wing concepts should apply, and we could then proceed and design that part of the wing shape to have a pressure distribution which has been shown to be suitable on a twodimensional aerofoil. This procedure is often applied, but we cannot yet say with confidence how far it will succeed in any given case. This will depend on how far it will be possible to find and to incorporate ef­ficient threedimensional supercritical flows in the central and tip regions.

Some very simple estimates of what might be reasonable design aims and assess­ments of various design pressure distributions in some more detail than in Fig. 4.8 have been made by D KUchemann (1970), following J A Bagley (1961).

The results show that supercritical aerofoil sections offer enough incentive to go further into this otherwise so awkward and complex matter: the possible advances beyond the subcritical state of technology may be quite large. For example, a successful outcome of current researches might lead to lift coeffi­cients which are half, or more, as much again as subcritical values; or to thickness-to-chord ratios which are increased by similar amounts; or to angles of sweep which are 5° to 10° lower; or to higher speeds, up to high-subsonic or low-supersonic Mach numbers. Similar estimates with similar results have been made by E C Polhamus (1971).

We may conclude that the aerodynamic design aims for one particular design condition are usually stated in the form that the required pressure distribu­tion over the surface is specified for a wing of given planform at a given mainstream Mach number. The wing shape to give this is then to be determined. Thus we are dealing with the Dirichlet problem rather than the Neumann problem for given shapes. Sometimes, the thickness distribution may be given before­hand. Then the pressure distribution over one surface only can be specified, usually that over the upper surface. Such design calculations have been car­ried out successfully so far mainly for subcritical flows. The RAE Standard Method and the RAE TSP Method have been specially designed for this purpose (see Section 4.4). But it must be remembered that numerically accurate solu­tions for threedimensional wings, such as those of the iterative method of С C L Sells (1976), can be obtained only for incompressible flow, because the compressibility effects can be treated only approximately and thus introduce an uncertainty. Errors may arise particularly in the centre and tip regions which, unfortunately, are just those which most require special treatment.

Thus there are some fundamental shortcomings in our design capabilities for swept wings, not only in supercritical flows but already in subcritical flows.

Any such design calculation must be followed up by fitting visoous regions in­to the inviscid flows so determined (see Section 4.5). This is primarily to check whether or not the flows are realistic and do not lead to unwanted flow separations. If they do, the design is obviously useless, and the process must be repeated. If no flow separations occur, such calculations will lead to some adjustments to the shapes previously determined. How to prevent se­parations by geometric design has been discussed by J C Cooke & G G Brebner (1961).

The procedure outlined so far deals with only one particular design condition; it can, in principle, be repeated for other design oonditions, and off-design oharaoterietios can also be determined. A final shape will emerge only when all these results have been taken into consideration in an overall synthesis.

Many of the actual design problems have already been discussed in the prece­ding Chapters. In this Chapter, we select and describe some particular pro­blems which arise in the aerodynamic design of classical and swept-winged air­craft. Again, we shall concentrate on methods which are based on the physics of the flows. In any case, detailed, and hence time-consuming, numerical me-

thods of analysis to determine the properties of given shapes cannot be used to start off a design; their place may be more in checking and refining designs already made or in determining the properties in off-design conditions. Nume­rical methods may also be used in conjunction with wind tunnel tests in an ite­rative process which may lead to step-by-step improvements in a design, as proposed by W Loeve (1974).