Transverse Flow Past a Slender Body of Revolution
The governing equation for the potential is Laplace’s equation (Eq. (8.105)),
![]() Э2Ф З^Ф 1 ЭФ ЗРФ dx2 + dr2 + r dr + r2 d62
Э2Ф З^Ф 1 ЭФ ЗРФ dx2 + dr2 + r dr + r2 d62
and the body boundary condition is given by Eq. (8.108b),
ЭФ
— (де, R, в) = – Q^a sin в (8.108b)
дт
The two-dimensional flow (in the y-z plane) of this problem resembles the flow past a cylinder, which was solved in Section 3.11. Therefore, the solution to this problem is modeled by a distribution of doublets of strength ju(jc) per length on the strip 0 s jt < /, z = 0. The doublet axes point in the negative z direction opposing the stream. The velocity potential and velocity components
are given by integration of the point elements (see Section 3.5) along the body’s length.
ф(г R – Ч_і_ Ґ /о 1104
Ф(Г’ в’Х)~ 4л l [(x – Xo)2 + r2f2 (8’118)
. ЗФ If’ (i(x„) sin edx0 З Ґ n(x0) sin в r2 dx0
qr{r, 0, x) – 3r – 4л. Jo [(jt _ Xo)2 + r2]3,2 4jr Jo [(jf _ Xo)2 + r2]5a
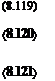 1 ЭФ If’ m(x0) cos 0 dx0 ^(r, и, х)-гдв- 4л ^ [(je _ Xo)2 + r2]3/2
1 ЭФ If’ m(x0) cos 0 dx0 ^(r, и, х)-гдв- 4л ^ [(je _ Xo)2 + r2]3/2
ЗФ -3 f’ ju(xo)(x – x0)r sin 0 dx0
To satisfy the body boundary condition, consider the flow in the crossflow plane (as shown in Fig. 8.28). This is simply the flow past a circular cylinder and its radial velocity component from Section 3.11 is
ju(x) sin 0 2л R2(x)
Thus the boundary condition at r — R becomes
 FIGURE 8.28
FIGURE 8.28
Crossflow model using doublet distribution along the x axis and pointing in the —z direction.
and the doublet strength is found to be
n(x) = 2nQ„aRx) = 2Q^aS(x) (8.122)
For small values of r (including the body surface) the solution is the flow past the circle in the crossflow plane and the perturbation potential and velocity components are
|
ф(г, в, x) – Q^ocR2 r |
(8.123) |
|
, . -7 sin в |
|
|
qr{r, в, x) – Q*aR2 2 r |
(8.124) |
|
, „ . л cos в qe(r, 6, x) = Q^aR2 2 r |
(8.125) |
|
. . . ЭФ sin в |
|
|
qx(r, e,x)~ -2Q„aRR ox r |
(8.126) |
Note that since the doublet strength is a function of x, the streamwise (axial) velocity component is unequal to zero.











