Two-dimensional supersonic flow past a wedge

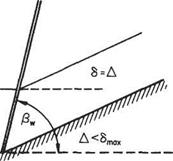
This can be described bearing the shock polar in mind. For an attached plane wave the wedge semi-vertex angle Д, say, Fig. 6.28, must be less than or equal to the maximum deflection angle (5max given by point F of the polar. The shock wave then sets itself up at the angle given by the weaker-shock case. The exit flow is uniform and parallel at a lower, in general supersonic, Mach number but with increased entropy compared with the undisturbed flow.

If the wedge angle Д is increased, or the free-stream conditions altered to allow Д > /3max, the shock wave stands detached from the tip of the wedge and is curved

ц> I

wminmmwwmwiwmwmm

Fig. 6.28

Fig. 6.29

from normal to the flow at the dividing streamline, to an angle approaching the Mach angle a long way from the axial streamline (Fig. 6.29).

All the conditions indicated by the closed loop of the shock polar can be identified:

В – on the axis the flow is undeflected but compressed through an element of normal shock to a subsonic state.

E – a little way away from the axis the stream deflection through the shock is less than the maximum possible but the exit flow is still subsonic given by the stronger shock. F – further out the flow deflection through the shock wave reaches the max­imum possible for the free-stream conditions and the exit flow is still subsonic. Beyond this point elements of shock wave behave in the weaker fashion giving a supersonic exit for streamlines meeting the shock wave beyond the intersection with the broken sonic line.

D – this point corresponds to the weaker shock wave. Further away from the axis the inclination of the wave approaches the Mach angle (the case given by point A in Fig. 6.27).

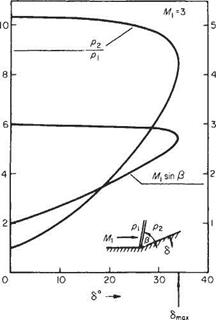
It is evident that a significant variable along the curved wave front is the product M sin /3, where /3 is the inclination of the wave locally to the incoming streamline. Uniform undisturbed flow is assumed for simplicity, but is not a necessary restric­tion. Now i < j3 < 7t/2 and M sin j3, the Mach number of the normal to the wave inlet component velocity, is thus the effective variable, that is a maximum on the axis, reducing to a minimum at the extremes of the wave (Fig. 6.30). Likewise all the other properties of the flow across the curved wave that are functions of M sin /3, will vary along the shock front. In particular, the entropy jump across the shock, which from Eqn (6.48) is

де 27(7 — 1) [М sin2/3 — l)3

K(7+l f 3

will vary from streamline to streamline behind the shock wave.

Fig. 6.30

An entropy gradient in the flow is associated with rotational flow and thus a curved shock wave produces a flow in which vorticity exists away from the surface of the associated solid body. At low initial Mach numbers or with waves of small curvature the same approximations as those that are the consequences of assuming AS— 0 may be made. For highly curved strong shock waves, such as may occur at hypersonic speed, the downstream flow contains shock-induced vorticity, or the entropy wake as it is sometimes called, which forms a large and significant part of the flow in the immediate vicinity of the body associated with the wave.