Unsteady Supersonic Flow

The linearized potential flow equations are exactly the same for the subsonic and supersonic flows. Equation 2.24 in its original open form was obtained as

This time we can use b2 = M2 — 1 as a parameter and perform a new Lorentz type of transformation (Miles 1959) to obtain the classical wave equation for the perturbation potential. Let us see the transformation based on a complex variables.

x = x, у = ifiy, z = ibz and t = t — Mx/ab2, b = v2M2 — 1 In transformed coordinates the potential equation reads as

1 02/

a2b4 0X2

t—-[1]!(Mx±g)

The solution of 5.57 in original coordinates reads as

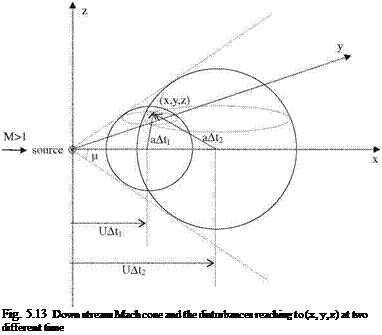The mathematical solution given with 5.58 is the expression for a source term in a supersonic flow. The ± appearing in exponent of 5.58 indicates that there are two different solutions for source. In order to identify the source solution which reflects the physics of the problem, we have to study the propagation of a dis­turbance in a supersonic flow as shown in Fig. 5.13. The speed of a wave front of a

perturbation in a supersonic flow placed at the origin is faster than the free stream. Therefore, the wave front is carried down in the direction of the free stream only in the positive x axis. For this reason, the tangent drawn from origin to the front surface at any time t makes a constant acute angle with the x axis as shown in Fig. 5.13. The locus of all these tangent lines is a conical surface called the Mach cone. The cone which is symmetric of this cone with respect to y-z plane is called the upstream Mach cone, and the opposite one is called the downstream Mach cone. Let At denote the time between its introduction to the flow and the present time t. If we call the half angle of the Mach cone as i = Mach angle, then we have

a At _ ( 1

sin i and i = sin

r U At MJ

Now, we can comment on the physics of the problem via Fig. 5.13. The comment will be based on the kinematic entities such as the free stream speed and the propagation speed of a disturbance placed in the flowfield. Knowing that the disturbance front travel as an expanding spherical surface, we can analyze the conditions under which the spherical front reaches at an arbitrary point (x, y, z) of the flowfield.

As seen in Fig. 5.13, there are two different spherical surfaces which pass through point (x, y, z). Both of these spherical surfaces are the products of the same disturbance created at the origin at time s and felt at the point (x, y, z) at two different times t1 and t2. With these timings the elapsed times are measured as A t1 = t1 — s and A t2 = t2 — s. The point (x, y, z), first feels the disturbance at time t1 from the frontal side, and at later time t2 the same point is effected by the back side of the disturbance. In other words, at the same instant t, point (x, y, z) feels the effect of two different disturbances created at the origin at two different times s1 and s2. This time, the durations elapsed between the creation of the disturbances and the present time t reads as Atj = t — sj and At2 = t — s2. In both cases, point (x, y, z) lies in the Mach cone. Any point outside of Mach cone does not feel any disturbance, therefore that region is called the zone of silence. Now, we can obtain the relations between the relevant timings using Fig. 5.13 and the interpretations made above.

a(t — s1)= [x — U(t — s1 )]2 + y2 + z2

(5.59 — a, b)

a(t — s2)= [U(t — s2)—x]2 + y2 + z2

From 5.59-a, b we can solve for sj and s2 as follows.

s1 = t—— ^(Mx — R) (5.60 — a, b)

ab 1

Considering the chronological order of the timings we have t > s1 > s2. We have also obtained the solution for the potential of the supersonic flow with expression 5.58. If we want to obtain a continuous solution in time, we have to include both of the solutions of 5.60-a, b for our perturbation potential as follows

/(x, y, z, t)=/(eixT1 + eixs2)/R. (5.61)

The solution we have obtained with 5.61 is going to be used as continuously distributed sources over the x-y plane to simulate the lifting surfaces undergoing simple harmonic motions. This distributed source has unknown distributed strength over the planform but in time it will oscillate simple harmonically. On the other hand, since the flow is supersonic, any point (x, y, z) in the flowfield is affected only from the points which are in its upstream Mach cone. We can now, write the integral expression accounting for all surface disturbances for the velocity potential as follows

/(x, y, z, t) = jjА(П, g)[(eixs1 + eixs2)/R]d£ dg (5.62)

V

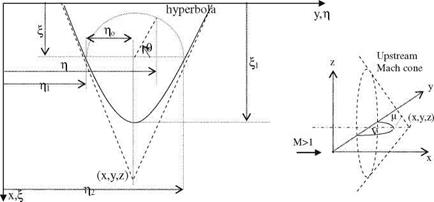
Here, А(П, g) is the unknown amplitude of the distributed source. The area over which the integral to be evaluated is a hyperbola defined as the intersection of the x-y plane with the upstream Mach cone of point (x, y, z), i. e. R = 0. This means, while z approaches zero we need to satisfy (x — П)2 – b2(y — g)2 — z2 = 0, which in turn means, it gives an equation of a hyperbola on x-y plane, because inter­section of a cone with a plane parallel to its axis is an hyperbola. The hyperbola and the pertinent geometric variables are shown in Fig. 5.14. The lower and upper integration limits for the double integral of Eq. 5.62 shown in Fig. 5.14 are defined as g1 and g2 as follows.

Fig. 5.14 Upstream Mach cone, and the integration area V

The integral limits in the chord direction can be considered as follows. We take the П = 0 point as the lower limit, and the apex of the hyperbola as the upper limit. Equation 5.63 tells us that g1 = g2 is the point for the upper limit, where the term under square root must be zero. That gives us

П1 = x ± b z (5.64)

Here, according to Fig. 5.14 x > П1, therefore in Eq. 5.64, +z is used for the lower surface, and —z is used for the upper surface. This information will be useful for evaluation of lifting pressure as lower minus upper surface pressure distributions.

Knowing the upper and lower limits of the integral 5.62, we can express

І1 g2

/(x, y, z, {) = J J А(П; g)[(e‘“T1 + e‘“T2)/Rdndg (5.65)

0 g1

Here, the exponents read as

S1,2 = t – 2[M(x – П)Т R)] and R = (x – П)2 – b2(y – g)2 + b2z2.

ap

(5.66 – a, b)

Values for g1 and g2 are used to give us R = by/(g – g1 )(g2 – g). In spanwise direction, as shown in Fig. 5.14, if we use variable в we obtain 2g = (g2 — g1)cosh + g2 + g1. With this transformation, and defining go = (g2 — g1)/2 gives us

dg = —go sin hdh and R = bgo sin в

Here, again according to Fig. 5.14, в = p at g = g1, and в = 0 at g = g2 . If we rewrite integral 5.65 in terms of new variables, it becomes

n1 p

/(x, y, z, t) =p А(П, y + go cos в)(е‘“Т1 + e‘“T2)dn dh,

00

S1,2 = t – 2[M(x – n)Tbgo sin в]

ab2

The velocity potential given by 5.67 is differentiated with respect to z to obtain the downwash at the wing surface. First, let us employ 5.67 to study the supersonic flow past a profile.