Weighting by the Difference to the Local Average Deformation
This weighting approach takes the deformation vectors Axinpii into account directly. It uses a function FindNeighbours (x, X, AX, d), which returns subsets of
less than d to x. In this case the distances are not weighted yet. The weights for the input point xinp, i are then calculated by
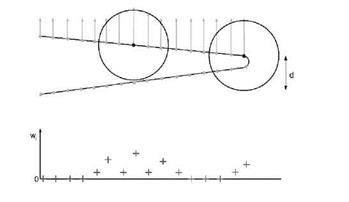
The idea is to develop an expression that favors the base points, the absolute deformation value of which is different to the average deformation value А. тпь of its neighbors. Another thought is that the nodes at the outer tips of a deforming body will get a higher weight, since at the tip the deformations reach usually their maximum and consequently differ strongly from the neighborhood mean. An approach which only takes the gradient into account would not result in a higher weight for the outer base points, because the deformation gradient would not have a peak at an outer base point. An example to illustrate this idea can be seen in figure 5. This simplified example shows why the approach leads to higher weights for the base points on the tip, the deformation vectors of which should not be neglected in the final base point set. It shows a tip body with a slight rotational deformation. The deformation vector with the largest value is on the tip of the body. The equidistant reduction algorithm from section 4.1 could easily fail to select the maximum deformation vectors. Because of the higher weight values at the tip this would happen less likely with the new algorithm.
This example shows a disadvantage of the algorithm as well. If the gradient of the deformation vectors is constant in a certain area, the weights will tend to zero. This will lead to a very low base point density in the next step. To get a lower border for the density, the final reduction method is combined with the equidistant reduction method. First a fraction fracequi of the desired ns, max base points is chosen by the equidistant algorithm, then the remaining base points and deformation vectors are selected with the weighted distance approach.
|
Fig. 5 Schematic example for weights w of the upper base points with their deformation vectors |