Wing Geometry Required for Elliptical Loading, Lifting-Line Theory

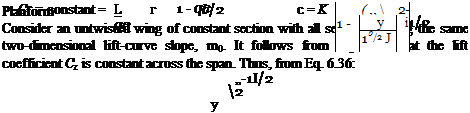It is shown in the previous section that elliptical-spanwise loading corresponds to minimum induced drag. There are three ways to design a wing to achieve elliptical – spanwise loading: (1) using a suitable wing planform, or (2) using wing twist, and it can be approximated (3) using a simple tapered planform.

where K = (T0/qsCt), which is a constant. Thus, the variation of the wing chord, c, with span, y, is given by:

K2 (b / 2)2

Eq. 6.48 states that if a wing is untwisted and of constant section with constant lift-curve slope, then an elliptical-lift distribution is generated if the wing has an elliptical planform. Furthermore, the elliptical-lift distribution occurs at any value of wing-lift coefficient. Thus, elliptical-lift distribution can be achieved in practice but at the cost of complexity of manufacture.

2. Twist

Assume (for simplicity) only that m0 = constant for any wing section. A geo­metric twist (varies with span) or an aerodynamic twist (aLo varies with span) or both are permitted. The induced angle of attack, a;, is a constant because of the elliptical-loading requirement. Then, from Eq. 6.45:

CL= mo(« -«i -“L0 ),

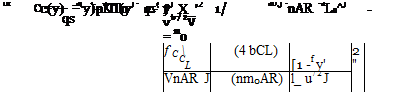and using Eqs. 6.36 and 6.42:

The local variation of wing chord as expressed by c(y) and wing twist as expressed by the absolute angle of attack aa(y) = [a(y) – aLo(y)] must be such as to satisfy Eq. 6.49 for all values of y. In particular, for a rectangular wing of constant sec­tion, Eq. 6.49 shows that an elliptical spanwise loading can be achieved provided that the geometric twist of the wing also varies elliptically with span. However, because CL does not cancel out in Eq. 6.49, this twist provides elliptical spanwise loading at only one (design) value of wing-lift coefficient. Again, as in the case of an elliptical planform, spanwise elliptical loading can be achieved at the cost of fabrication complexity.

3. Tapered Wing

Recall from Eqs. 6.31 and 6.44 that a wing of arbitrary planform with arbitrary spanwise loading has an induced drag that is a factor (1 + 5) larger than that for elliptical loading. A straight-tapered wing with a taper ratio of about 0.4 has a value of 5 or about 0.01. Thus, this wing—which is relatively straightforward to manufacture—has an induced-drag coefficient that is only about 1 percent above the minimum. We verify this conclusion by running Program PRANDTL for various taper ratios and examining the values of induced drag in the neigh­borhood of a taper ratio of 0.4.