A THEORETICAL JUSTIFICATION OF THE APPROACH

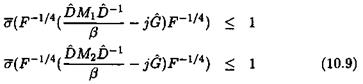Let D and G some scaling matrices satisfying equation (10.6) at two frequencies u) and u>2- Let D and G the corresponding scaling matrices, computed with Lemma 2..1. D and G thus satisfy:

with F = In + G2. Assume that uj and ш2 are sufficiently close, so that a first order approximation of M(jul) is valid:

M(j((jj + (1 — A)u>2)) и XM(jbj) + (1 — )M(jw2) V А Є [0, 1]

The spectral norm a is convex, i. e. the following relation is satisfied for А Є [0, 1]:

сг(АЯ! + (1 – A)H2) < Аст(Яі) + (1 – A)a(H2) (10.10)

where Hi and Н4 are any fixed matrices. Equation (10.9) consequently implies that (V А Є [0, 1]):

As a consequence, (D, G) scaling matrices, synthesized on frequencies u>і and u>2, are valid on the whole segment [wi, шг] when a first order approximation of M(jut) is valid on this frequency interval.

3.2 CONCLUSION

A first solution is to choose a sufficiently fine frequency gridding (ші)іє[і, лг]> so that the first order condition of subsection 3.2 is satisfied at all points of the frequency gridding:

+ (1 – A)wi+1)) » Ш(М) + (1 – X)M(jwi+i) VA Є [0, 1]

(D, G) scaling matrices are then computed, which simultaneously work at frequencies щ and u>j+i, in order to compute (D, G) scaling matrices, which are valid on the whole interval [w*, cuj+i].

Nevertheless, this approach will often need an unnecessarily fine fre­quency gridding, since the above equation is just a sufficient condition for guaranteeing the property that (D, G) scaling matrices, which simultan­eously work at frequencies щ and ші+i, also work on the corresponding interval. An alternative solution is to choose a looser frequency grid­ding (u>i)ie[i, jv]: (D, G) scaling matrices, which simultaneously work at frequencies and are here again computed, and the validity of these D, G scaling matrices on the frequency segment is checked only a posteriori. In this new context, a solution is to use Proposition 4..2 of the following section.