Aerodynamic Force Analysis

This chapter will examine aerodynamic forces acting on a body, and how they are related to the properties of the flow-field. A major goal is to rigorously relate the lift, drag, and sideforce components to the flow-field on a closed bounding surface which is either on the body surface itself (near-field force), or arbitrarily far from the body (far-field force).

Another major goal is to simplify the far-field forces using suitable simplifications and idealizations of the flow-field, in particular the trailing vortex wake. This will produce expressions for the lift, drag, and sideforce which involve the trailing vortex wake alone. It will also allow the decomposition of the drag force into profile-drag and induced-drag constituents, and thus enable the optimization of aerodynamic configurations for minimum induced drag.

5.1 Near-Field Forces

5.1.1 Force definitions

The near-field aerodynamic force F on a body is the total force that the fluid exerts on its surface Sbody, as shown in Figure 5.1. This can be decomposed into pressure normal forces and viscous stress forces,

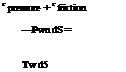F

F

F pressure Ffriction

where pw, Tw are the pressure and viscous stress vector acting on area element dS, with unit normal n. Replacing — pw with pTO—pw in the second pressure integral is allowed because the uniform pressure pTO does not exert a net force on a body. This follows from the identity◦ n dS = 0, valid for any volume.

Choosing the x-axis to be aligned with the freestream, V = X, the streamwise drag force component is

then D — F • X, which has pressure and friction contributions, as shown in Figure 5.1.

D=	F • X — Dpressure + Dfriction	(5.4)
Dpressure =	(p<x> — Pw) n • X dS	(5.5)
Dfriction =	(Я Tw • X dS	(5.6)

W t_*.

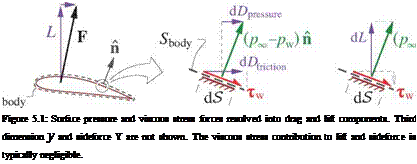
The transverse-horizontal and transverse-vertical components are the sideforce Y and the lift L.

Y = F ■ y ~ (pTO – pw) n ■ y dS	(5.7)
L = F ■ z ~ U (pTO – pw) П ■ z dS	(5.8)

The viscous stress contributions to Y, L will be neglected in the subsequent discussion, since at high Reynolds numbers they are typically negligible compared to the pressure contributions.