APPLICATIONS OF LAPLACE TRANSFORMATION

The method of Laplace transformation can be applied to a number of aeroelastic problems. In this chapter the mathematical background will be outlined briefly, and’ its applications will be illustrated by examples in gust response and flutter.

10.1 LAPLACE TRANSFORMATION

The method of Laplace transformation is extremely powerful in treating certain response problems. Its mathematical foundation and refinements cannot be treated in this book because of the limited space. However, there exist many good books on this subject.101”10-7 Hence, in the following, we shall only quote the rules of the method of Laplace trans­formation, and give some heuristic derivations to help understand them.

The Laplace transform of a function F(t), which vanishes for t < 0, is defined by the integral

&{F{t)s} =^e~slF{i) dt

The inverse transform is given by the equation

F(t) = ——. f es,£F{Fs) ds (c > a)

2m Jc—i oo

where a is a real number greater than the real parts of all the singular points of SF{Fs). Whenever these integrals exist, F(t) and ££{Fs) are called the original and the image, respectively. If there is no confusion, the image £f{Fs} will be written as ^£{F).

The conditions for the validity of the reciprocal relations 1 and 2 depend much on the sense of integration of the integrals. If the integrals are taken as Cauchy principal values in the Riemannian sense, a set of sufficient conditions which guarantees the validity of the Laplace trans­formation is

1. The integral 1 is absolutely convergent in the region Rl. s > a.

2. Fit) is of bounded variation in any finite interval, and F(t) = 0 for t < 0.

If these conditions are satisfied, the reciprocal relations between F(t) and £F{Fs) are essentially unique.

Example 1. Let F(t) = l(t); i. e., Fit) — 1 when t > 0, Fit) — 1/2 when t = 0, and F(t) = 0 when t < 0. Then

&{Чф} = e~sldt=-~e-st Jo S 0

Hence, when R1 s > 0,

Example 2. Let F(t) = ekt when t > 0. Then

f OO,

FF{ekt} = e~st eu dt =—————- (R15 > R1 k)

Jo s — к

Following van der Pol and Bremmer,10-7 we shall regard the method of Laplace transformation as a language. In actual applications we first transpose the problem under consideration, which is formulated in terms of the variable t, into a new problem in the variable s; i. e., the functional relations (such as differential and integral equations) in which the problem is first stated are transformed into their operational equivalent. This is done by multiplying the given relation or relations by the function e~st and then integrating from t = 0 to t = oo. This is a transition from the t language to the s language. In many problems the new problem in the ■s language is considerably simpler than the original one in t, and therefore leads to an easier solution. Once the problem is solved in terms of s, it only remains, as the second stage of the method, to translate the і solution back into the physical language of t.

For the purpose of such translation between the s and t languages, a “dictionary” is necessary. An abridged one is given in Table 10.1. A complete dictionary is given by Erdelyi.108

The user of the language must know the “grammatical” rules by which the 5 and t languages are translated into each other. A few basic rules are quoted below. They are constructed on the basis of Eqs. 1 and 2. But, in applying the dictionary and grammar, these integrals need no longer be used explicitly.

Linearity. The Laplace transformation is linear; i. e., if A and В are constants, then

££{A F(t) + В G(t)} = A ££F) + BF£{G)

This follows from the definition of the transformation. Hence, a multi­plication of the original by any constant A corresponds in the s language to a multiplication of the image by A, and the image of the sum of two originals is equal to the sum of the separate images.

i. e.,

.5?{sinh kt} = —

S’" K~

Similarity Rule. Let

JF{F(t)} = f(s) (a < Rlj < oo)

Then, if A is a positive real constant,

SF{F{k)} = j j (Aoc < Rb < oo)

Example 4.

-5P{cos t} = – r-y—г; SO ^{cos kt} — S

sz + 1 sz + кг

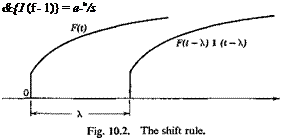
Shift Rule. If /(s’) is the Laplace transform of F(t), then e >sf(s), Я > 0, is the transform of the function F(t — Я) 1 (t — Я), where 1 (t — Я) is the unit-step function.

This is seen from the following equation:

ГF(t – Я) l(r — X)dt = Ге-Н F(t – Я) dt = e~u (“e~a F(t) dt JO J A Jo

Note that

(0 when t <X

F(t – Я) 1 (t — A) = !

1 F(t — A) when t > A

The function F(t — Я) 1 (t — A) is obtained by shifting the original function F(t) to the right through a distance X (Fig. 10.2).

Example 5. Since

^{1(0} =

we have

and the Laplace transform of a square wave of band width 2a is (Fig. 10.3)

&{1 (t — A) —(t — A — 2a)} = і (e’u – е~и’ш)

= – e-<A+als sinh as s

Example 6. In automatic control of airplane lateral stability, it is sometimes advantageous to gear the rudder angle 6r to the yawing acceleration ip, but lagging by a specified time interval, т:

The factor e_TS is often called a lag operator.

Attenuation Rule. If

£Є{Р(()} = f(s) (a < R1 j < oo)

then

£’{e-uF(t)}=f(s + A)

■ПШ =Ms) = Л(*)

This follows directly from substitution into the definition integral (Eq. 1).
Convolution Rule. If F*(/) and F2(/) are piecewise continuous and

then

fi(s)f2(s) == ^{F^tfF^t)} (max (oq, a2) < R1 s < oo) where Fx{t)*F2(t) is the so-called convolution integral:

F&YF&) = f Vx(r) F2(t – r) dr = Pfx(/ – r) F2(r) A-

Jo Jo

This is probably the most important of all rules.

A formal derivation of this rule is as follows:

J

* 00 /*00

e~m FJu) du I e~nF4p)do

0 Jo

= f00 f °V(“+,,,S Fx(u) F2(v) du dv Jo Jo

Introducing a new variable t — и – j- v, and letting the variables (и, v) be transformed into (и, /), we have

fi(s)Ms) =j^ J e~ts Fx(m) F2(/ – u) du dt

Fx(m) F2(/ — u) du

The role of iq and F2 are obviously interchangeable. Hence, the last equation is equal to

Ms) 40) = І е~л dt f Fx{t – u) F2(u) du Jo Jo

The last two equations state the convolution rule.

Differentiation Rule. Let

JF{F(t)} = f(s) (a < R1 j < oo)

If F(/) has a derivative F'(t) for t > 0, and if the Laplace transform of F'(t) exists, then

nnt)} = Ф) – Я0 +)

where F(0 +) means the limit lim F(0 + є), є > 0.

e—>0

Hence, a differentiation of the original with respect to t corresponds to a multiplication of the image by a factor s.

A formal derivation of this rule is as follows. By a formal integration by parts, we have

ЩПО} = Гe~st F'(t) dt
Jo

‘ Д0

provided that the limit of e~siF(t) tends to zero as t —> cc.

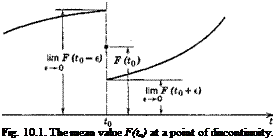
Let us remark that the continuity of the function Д0 is important for the validity of the above formula. If Д0 is continuous except for an “ordinary” discontinuity at t — t0, we would have

ЩРЩ = sf(s) – ДО +) – [Дг0 + 0) – Дг0 – 0)] є"’"8

where the quantity in the brackets is the jump of Д0 at t = t0.

Repeated application of the above rule leads to the following: Successive Differentiation Rule. Let the function F(t) be n times differentiable for t > 0, and let the Laplace transform of the uth derivative Fln)(t) exist for a < R1 s < oo. Then F(t) has a Laplace transform for all s, R1 s > a, and