BASIC FORMULATION

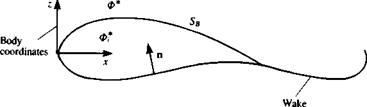
Consider a body with known boundaries SB, submerged in a potential flow, as shown in Fig. 9.1. The flow of interest is in the outer region V where the incompressible, irrotational continuity equation, in the body’s frame of reference, in terms of the total potential Ф* is

V2<l>* = 0 (9.1)

Following Green’s identity, as presented in Section 3.2, the general solution to Eq. (9.1) can be constructed by a sum of source о and doublet p distributions placed on the boundary SB (Eq. (3.13)):

Ф*(х, у, Z) = – [o0) – pn • V0)] dS + Фоо (9.2)

Here the vector n points in the direction of the potential jump p which is normal to SB and positive outside of V (Fig. 9.1), and Ф„ is the free-stream potential:

Фоо = І/».* + К, у + WLz (9.3)

This formulation does not uniquely describe a solution since a large number of source and doublet distributions will satisfy a given set of boundary conditions (as discussed in Chapter 3). Therefore, an arbitrary choice has to be made in order to select the desirable combination of such singularity elements. It is clear from the previous examples (in Chapters 4-8), that for simulating the effect of thickness, source elements can be used, whereas for lifting problems, antisymmetric terms such as the doublet (or vortex) can be used. To uniquely define the solution of this problem, first the boundary conditions of zero flow normal to the surface must be applied. In the general case of three-dimensional flows, specifying the boundary conditions will not immedi­ately yield a unique solution because of two problems. First, an arbitrary decision has to be made in regard to the “right” combination of source and doublet distributions. Secondly, some physical considerations need to be introduced in order to fix the amount of circulation around the surface SB.

These considerations deal mainly with the modeling of the wakes and fixing the wake shedding lines and their initial orientation and geometry. (This is the three-dimensional equivalent of a two-dimensional Kutta condition.) However, based on the previous examples, it is likely that the wake will be modeled by thin doublet or vortex sheets (Fig. 9.1) and therefore Eq. (9.2) can be rewritten as

Ф *(x, y,z)=—j ;

‘тЛ •’body+wake