Our heavyweight helicopter equal in the world does not have
In Rostov started production of the most load-lifting rotary-wing car The Russian holding «Helicopt[...]
Cone versus Flat-Plate Boundary-Layer Transition
The simplest way to take into account the shape of a slender configuration for stability and transition considerations is to approximate it by a conical configuration.
Considerable confusion arose around this approach [11]. Older experimental data had shown consistently that cone flow exhibits higher transition Reynolds numbers than planar flow, in any case for Mach numbers between 3 and 8 [11]. But stability analyses, first by L. M. Mack [36], and then by M. R. Malik [37], did show that disturbances grow slower on flat plates than on cones.
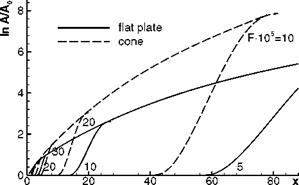
We illustrate this in Fig. 8.7 with results obtained with linear stability theory by A. Fezer and M. Kloker [38]. From these results, with small initial disturbance levels, one should expect that the transition Reynolds numbers on sharp cones are smaller than on flat plates.
|
Fig. 8.7. Transition on a flat plate and on a sharp 7° half-angle cone [38]: results from linear stability theory show the different amplitude growths of individual disturbance amplification curves and envelopes. In both cases Me = 6.8, Re’U = 5.72-106 m-1, Tw = 975 K, hypersonic viscous interaction being neglected, 2-d disturbances, various frequency parameters F. |
This was indeed found with experiments in the “quiet tunnel” of NASA Langley, Sub-Section 8.3.2, at M = 3.5 [11]. However, at M = 8 K. F. Stetson found later (with cooled model surfaces) transition on the cone to occur— again—somewhat more downstream than on the flat plate. Different disturbance levels and different instability phenomena on the cone and on the flat plate are the cause of the diverse observations. In [38] also spatial direct numerical simulation (DNS) was applied. For M= 6.8 and radiation-cooled surfaces the result was obtained that in principle the transition mechanisms work in the same manner on the cone and the flat plate. But on the cone fundamental breakdown is accelerated by the decreasing propagation angle of the secondary 3-D wave, while oblique breakdown probably is the dominant transition mechanism on the flat plate.[134]
A direct first-principle connection of these results and the results of linear stability theory to the different mean-flow patterns on a cone and a flat plate has not been established so far, although second-mode disturbances are tuned to the boundary-layer thickness [11]. On the cone the axisymmetric boundary layer is thinner than on the flat plate due to the Mangler effect, Section 7.2, and the streamlines in the boundary layer show a divergent (conical) pattern compared to the parallel flow on the flat plate. In addition we have, with the same free-stream conditions in both cases, a smaller boundary-layer edge Mach number and a larger edge unit Reynolds number on the cone than on the flat plate. We should note, however, that a conical vehicle configuration in reality will have a blunt nose.
