Constant chordwise ordinates

If the aerofoil is thin, and by definition this must be so for the small-disturbance conditions of the theory from which Eqn (6.118) is derived, the implication of this restriction is that the aerofoils are of similar shape in both planes. Take first the case of C = 1, i. e. £ = x. This gives D = В = y/l — M^ from Eqn (6.125). A solution of

Laplace plane Velocity potential Ф=(/|~М*)ф

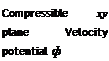Fig. 6.35

Eqns (6.118) or (6.119) is found by applying the transformation rj = л/1 — M2 у (see Fig. 6.35). Then Eqns (6.122) and (6.123) give

дф	В	дФ
Ру.	y=о A	.9n.

V = U ^ = c °°dx

7) = 0

= — XJ AUc°dt

but D — B, since D/C = В and C = 1.

For similar aerofoils, it is required that dy/dx = dry/d£ at corresponding points, and, for this to be so:

the relationship between lift coefficients in compressible and equivalent incompress­ible flows follows that of the pressure coefficients, i. e.

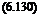
ЖЖ

This simple use of the factor у/1 — Mj, is known as the Prandtl-Glauert rule or law and ^/1 — Mj, is known as Glauert’s factor.

Constant normal ordinates (Fig. 6.36)

Glauert,* however, developed the affine transformation implicit in taking a transformed plane distorted in the ^-direction. The consequence of this is that, for a thin aerofoil, the transformed section about which the potential Ф exists has its chordwise lengths altered by the factor 1/C.

With D = 1, i. e. Tj = y, Eqn (6.131) gives

Ч=7т=їгг (6131)

Thus the solution to Eqn (6.118) or (6.119) is found by applying the transformation and, for this and the geometrical condition of Eqns (6.122) and (6.123) to apply, A can be found. Eqn (6.122) gives

<=u~t

By substituting Ф = Аф, Eqn (6.121), у = rf, Eqn (6.131), but from Eqn (6.122)

, = UndT)= U^dy c A dC A dxV 00

To preserve the identity, A = yj — Mand the transformed potential Ф = y/X – MIq ф, as previously shown in Eqn (6.127). The horizontal flow perturb­ations, pressure coefficients and lift coefficients follow as before.

Glauert explained the latter transformation in physical terms by appealing to the fact that the flow at infinity in both the original compressible plane and the trans­formed, ideal or Laplace plane is the same, and hence the overall lifts to the systems are the same. But the chord of the ideal aerofoil is greater (due to the £ = x/y/l — distortion) than the equivalent compressible aerofoil and thus for

an identical aerofoil in the compressible plane the lift is greater than that in the ideal (or incompressible) case. The ratio Lc/Lj is as before, i. e. (1 — A/^)_1/2.

Fig. 6.36

* H. Glauert, The effect of compressibility on aerofoil lift, ARCR and M, 1135, 1927.

Critical pressure coefficient

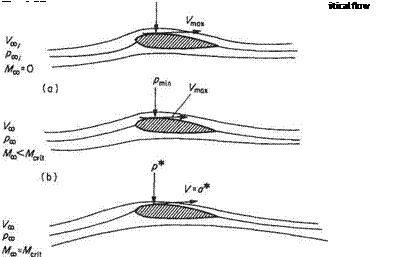
The pressure coefficient of the point of minimum pressure on an aerofoil section, using the notation of Fig. 6.37b, is

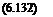_ Pmin Рос

Ртпіп “I __

1,1 ,

but since 2#»^oo = 2^P°°^oo’ Eqn (6.132) may be written

The critical condition is when first reaches the sonic pressure p* and Mx becomes Mcri, (see Fig. 6.37c). is then the critical pressure coefficient of the aerofoil section. Thus

An expression for p*lpoc in terms of Merit may be readily found by recalling the energy equation applied to isentropic flow along a streamline (see Section 6.2) which in the present notation gives

OO і ЭО______ і _____

2 7-1 27-1

(6.135)

In this expression Merit is the critical Mach number of the wing, and is the parameter that is often required to be found. CPcrit is the pressure coefficient at the point of maximum velocity on the wing when locally sonic conditions are just attained, and is usually also unknown in practice; it has to be predicted from the corresponding minimum pressure coefficient (CPi) in incompressible flow. CPi may be obtained from pressure-distribution data from low-speed models or, as previously, from the solu­tion of the Laplace equation of a potential flow.

The approximate relationship between ^7>crit and CPi was discussed above for two­dimensional wings. The Prandtl-Glauert rule gives:

(6.136)

A simultaneous solution of Eqns (6.135) and (6.136) with a given Сл yields values of critical Mach number Merit-