EFFECT OF FLIGHT CONDITION ON THE LONGITUDINAL MODES OF A SUBSONIC JET TRANSPORT

In Sec. 9.1 we gave the representative characteristic modes of a hypo­thetical subsonic jet airplane for a single set of parameters. It is of consider­able interest to enquire into how these characteristics are affected by changes in the major flight variables—speed, altitude, angle of climb, and stability margin. It is also of interest to establish the nature of the approximation dpjdz == 0. In this section we present numerical results that illustrate the above features.

9.4.1 EFFECT OF SPEED

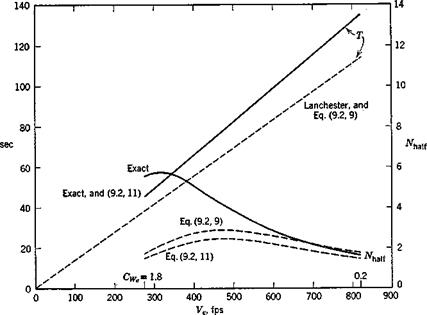
When the speed is changed in horizontal flight, the matrix (9.1,1) previously used is still applicable. All the assumptions made in Sec. 9.1 are retained—in particular, no Mach number effects are included—and hence the only quantities that vary are CLe, CDe, GTy, @Da , and t*. The eigenvalues and eigenvectors of (9.1,1) have been calculated for a range of speeds, and the variations of the period and damping of the two modes are given in Fig. 9.4. The Lanchester approximation to the phugoid period (9.2,5) is shown for comparison, as well as approximations (9.2,9), (9.2,11), and (9.2,14) to the phugoid and short-period modes, respectively.

The speed domain shown corresponds to a range of Gw from.2 to 1.8. This is somewhat larger than that over which one might expect the theory to be accurate. The highest speed corresponds to M = .82 at which com­pressibility effects would be expected to be present in Glx> gd„ , and CTy, and possibility in and G. On the other hand, at the large CL corre­sponding to the lowest speed, flow separation effects might be expected to occur on the cruise configuration in the absence of boundary layer control, affecting several of the derivatives.

(а)

(Ь)

The phugoid period is seen to behave qualitatively as predicted by Lan – chester’s theory, and the usefulness of the approximate theories for pre­dicting it is evident. Not so for the damping of the phugoid however, for which the approximate theories fail to predict the severe loss of damping at low speeds, where the number of cycles to half amplitude increases to nearly six.

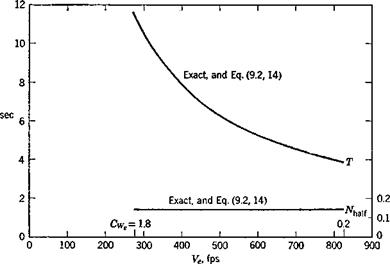
The short-period mode has essentially constant nondimensional eigen­values [note that CWe does not appear in (9.2,14)]. The variation shown in T comes almost entirely from that of t* = cj2Ve. The approximation given by

(9.2,14) is to the accuracy of the graph indistinguishable from the exact solution.

At the lowest speed the separation of the periods of the two modes is much less than at high speeds, their ratio at 274 fps being only 3.9 by contrast with 34.8 at 821 fps.

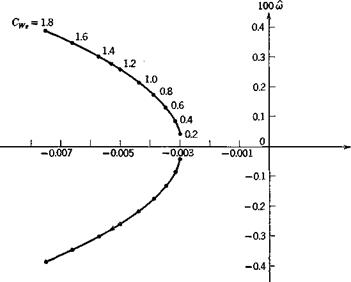
Figure 9.5 shows the root-locus of the phugoid mode. That for the short – period mode is virtually a pair of conjugate points and is not shown.

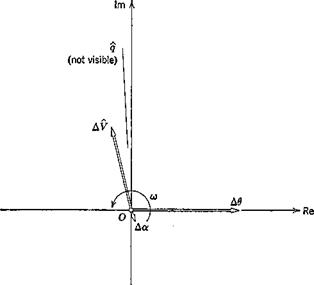
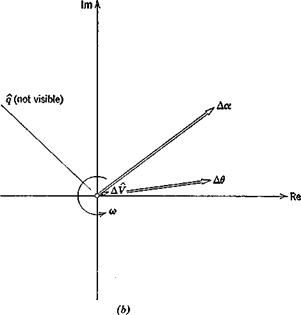
Figure 9.6 shows how the modal characteristics (the eigenvectors) have changed at the lowest speed. The most significant feature is that appreciable Да has appeared in the phugoid and Af’ in the short-period mode. This can be traced to the fact that the periods of the two modes are much closer to one another at this speed, and hence that the coupling between the previously

100 n

Fig. 9.5 Root locus—phugoid mode, variable Ow.

(а)

lightly-coupled degrees of freedom is stronger. That is to say, a variation of a at the short-period frequency can induce an appreciable speed change under these conditions and the pitching moment variation during the phugoid (associated mainly with Cmfl) can induce appreciable changes in a. Now we arrived at the approximations (9.2,9) and (9.2,14) by ignoring Да in one mode and AF in the other. It therefore follows that the approximations might be poorer at low speed than at high speed. This is clearly shown for the phugoid damping in Fig. 9.4a, but the approximations to the phugoid period, and to the short-period mode, are not appreciably worse at low speed than at high speed.