EFFECT OF FLIGHT-PATH ANGLE

To calculate the stability characteristics for nonhorizontal flight it is necessary to neglect all the г derivatives, and use the system matrix of (5.13,19). The basic aerodynamic assumptions made in the following calcu­lations are the same as those used in Sec. 9.1 but the following important difference should be noted—the thrust and lift are no longer equal to the drag and the weight, respectively. Instead at angle of climb ye we have, when ccy = 0,

-=-ft-r (94Д)

Since with the assumptions of the model used, CT = —2GTe, this derivative, and hence the coefficient an of the matrix, vary strongly with ye. It is also

34

32

30

28

26

24

22

20

18

16

14

12

10

8

6

4

2

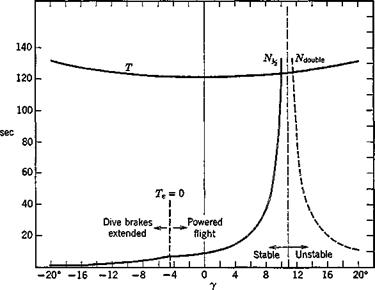
necessary to note that for negative flight-path angles (diving flight) greater than a few degrees (9.4,1) would require negative thrust. For this range of ye we have assumed for the purposes of the example that Te is zero and that dive brakes are extended to provide the necessary drag, i. e. that

CDc = —@we sin Ye (9.4,2)

Thus for ye less than the power-off glide angle, an = (CwJ/u) sin ye. The main results of calculations of the eigenvalues are shown on Figs. 9.12 and 9.13 for the constant values GWe = .25, pe = .000889, Kn = .10. The short-

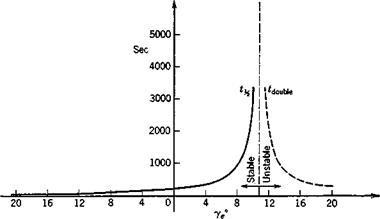
Fio. 9.13 Variation of the time to half amplitude of the phugoid mode with y.

period mode is not significantly affected by ye, but the phugoid is very much. Figure 9.12 shows the variation of its period and damping over the range —20 <ye < 20°. Although the period varies only slightly, the damping deteriorates rapidly with increasing climb angle until the mode becomes unstable above 10.8°. At 20° climb angle the number of cycles to double amplitude has decreased to about 2.2, but because of the long period the time to double, as shown on Fig. 9.13, is still very long—289 sec.

This behavior of the phugoid damping is approximately predicted by the two-degree-of-freedom analysis. If ye be retained from the beginning, with GT = —2CTg for constant-thrust powered flight, the same method that was used to obtain (9.2,9) yields for this case the characteristic equation

s2 + 7- (2С’/Л – CWe sin ye)s + (CWe cos2 ye – CDe sin ye) = 0 (9.4,3)

The coefficient of s, which gives the damping, decreases as ye increases, and

346 Dynamics of atmospheric flight vanishes at the critical angle

У, =sin-x^ (9-М)

ent /7

bWe

For the example, this is 8.6°, somewhat less than the correct value of 10.8° obtained from the complete system of equations.

The unstable phugoid can be shown to be entirely a consequence of the thrust law assumed. If the propulsion system were one of constant power TV instead of constant thrust T, the value of CTy would be —3GT^ instead of —2CTt [see (7.8,5)]. In that case the coefficient of s in (9.4,3) turns out to be 3CDJ2/n, a positive number almost independent of climb angle, and the approximate theory indicates no important change of phugoid char­acteristics with angle of climb. Values of CTy intermediate between the two values used above would give less reduction in the damping than shown in Fig. 9.12.