EFFECT OF SPEED DERIVATIVES
In the preceding examples, all the speed derivatives except GTfr were assumed to be zero. Now speed effects are highly dependent on the configuration, and for subsonic airplanes result from both aeroelastic and compressibility effects. They vary widely from one vehicle to another, and can change rapidly with Mach number (implying that the small-disturbance theory is very restricted in that case). It is not therefore feasible to give
|
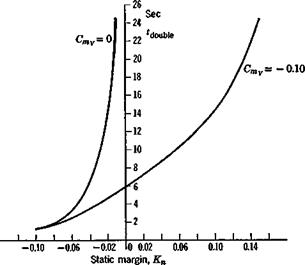
Fig. 9.19 Time to double of the divergent mode. |
any generally useful results for speed effects. There is one point, however, which is worth exploring, and that is the effect of Gmp on the roots. Equation
(9.3,3) shows that this derivative can affect the static stability, negative values producing a reduction in the stability boundary hs [see (6.4,26)]. To illustrate this, the value of Cmp has been set equal to —.10 in (9.1,1) and the eigenvalues found for the same range of Kn as used in the previous example. This value of Gmp is quite representative of what may occur at high subsonic Mach number. The root loci obtained look much like those presented in Fig. 9.18. The short-period mode is changed only slightly, but the phugoid has an important difference; namely, the divergent branch DE crosses the axis at Kn = .20 instead of at zero. Thus there is an unstable divergence over the whole of the C. G. range used in the example. The nature of this divergence is seen in Fig. 9.19, which shows the time to double amplitude. The divergence associated with this value of Cm is not very rapid for reasonable design values of Kn, i. e. Kn > .03, for then double > 8 sec and the airplane would not be unmanageable. The unstable mode is one involving primarily the speed and flight-path angle (of opposite sign) so that it represents either a climb at increasing climb angle and decreasing speed, or a dive of increasing speed and dive angle. The latter is what was called a “compressibility dive” at the end of World War II. The nonlinear features rapidly take over control of these motions as Д7 increases. For the climb divergence, the reduction of speed and Mach number take the vehicle back toward the incompressible regime and a reduction in Cmy whereas the dive case leads to increasing M and possibly an aggravation of the divergence.