EFFECT OF STATIC MARGIN

It was indicated in Chapter 6 that the single most important aerodynamic characteristic for longitudinal stability is the pitch stiffness Gm^, and that it varies strongly with the C. G. position, i. e.

Gma = GfJh – hn)

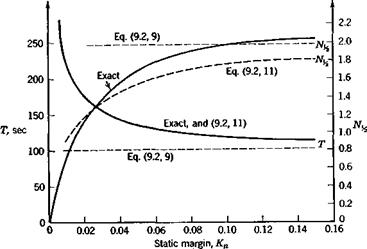
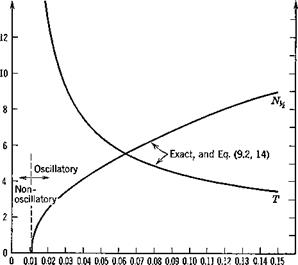
where the static margin is Kn = hn — h. The effect of this parameter is demonstrated by using (9.1,1) with variable Kn. The results for all other data the same as in Sec. 9.1 are shown on Figs. 9.16 to 9.19. Figure 9.16 shows that the phugoid period and damping vary rapidly at low static margin, and that the approximation (9.2,9), which does not include the effect of the pitch stiffness, is useful only at large Kn. Approximation (9.2,11), however, gives the trends with Kn quite well. The period goes to infinity, and Ni^ to zero at a value of Kn slightly greater than zero. Figure 9.17 shows the variation of the short-period roots. These too vary strongly with pitch stiffness, the mode becoming nonoscillatory at Kn slightly less than.01.

Fig. 9.16 Variation of period and damping of phugoid mode with static margin.

0.26

0.24

0. 22

0. 20

0.18

0.16

0.14

0. 12

0.10

0.08

0.06

0.04

0.02

0

The approximation of (9.2,14) is seen to be excellent over the whole oscillatory range.

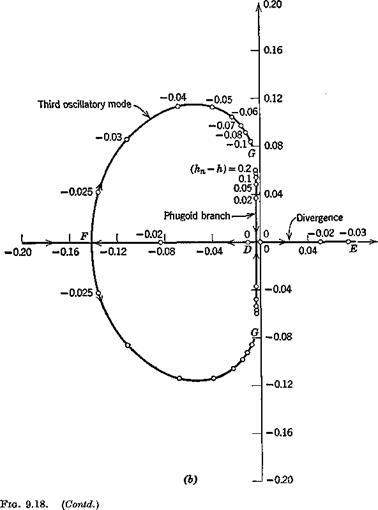
Additional insight into the behavior of the modes is obtained from the root-locus plots of Fig. 9.18. Figure 9.18a shows that the damping n of the short-period mode remains essentially constant as Kn decreases, while the fre­quency со decreases to zero at Kn between.01 and.02 (point A). The root locus then splits into a pair of real roots, branches A В and AG of the locus. These represent damped aperiodic modes, or subsidences. Figure 9.186 shows that the phugoid mode behaves similarly as the C. G. is moved backwards towards the neutral point. At point D, when the C. G. is just forward of the N. P., the oscillatory phugoid also degenerates into a pair of aperiodic modes, the branches DF and DE of the locus. DF is a subsidence and that portion of DE to the right of the origin represents a divergence—i. e. the airplane is statically unstable when Kn is negative.

The behavior of the roots is quite interesting for h > hn + .02. The branch AB of the short-period mode and the branch DF of the phugoid “collide” at F when the C. G. is between 2 and 2|-% of c behind the N. P. A new oscil­latory mode then appears corresponding to the branches FG of the locus. This is a stable oscillation whose damping and period are intermediate between those of the two parent modes. The eigenvector for this mode shows that all three degrees of freedom Д F, Да, Дв are significantly excited, and
hence there is no simple approximation to it. Since the range of C. G. positions in which this mode occurs is that for which there is already one unstable root (DE), it is of academic interest only.

It was shown in Sec. 9.3 that the criterion for static stability is (9.3,3). The calculations presented in Fig. 9.186 verify this conclusion, since in the example Cmy = 0 and the criterion reduces to Kn > 0. When the C. G. is aft of the N. P. the rate of divergence of the unstable mode is as shown in Fig. 9.19 (curve for Cmy = 0). The time to double rapidly decreases with decreasing Kn to values-too short to be manageable

100 w