Far-Field Forces

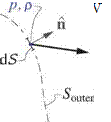
Consider the indented control volume shown in Figure 5.3, which has the body outside of it topologically. Since the volume is empty, the integral momentum equation (1.28) can be applied to it. Assuming steady flow, and eliminating the gravity force pf by re-defining p to exclude the hydrostatic pressure, we have

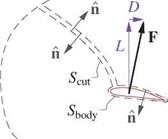
where the contour integral can be broken up into three Sbody, Souter, and Scut pieces indicated in Figure 5.3. §[]dS = § [ ]dS + § [ ]dS + []dS = 0

body outer cut

Since the two parts of Scut have equal and opposite П vectors its contribution vanishes.

[]dS = 0 (5.11)

cut

Furthermore, Sbody is defined to lie on the body’s solid surface where V ■ П = 0, so that the Sbody integral upon comparison with (5.1)-(5.3) is seen to be the body force F.

§ [ p(V■ n)V + pn – T ■ n ] dS = § [ Pwn – rw ] dS = F (5.12)

body body

The integrand above differs in sign from (5.1)-(5.3) because here n is in the opposite direction, as can be seen by comparing Figures 5.1 and 5.3.

Combining (5.11) and (5.12) with (5.10) then gives an expression for the body force which involves only the Souter contour. This is known as the Integral momentum theorem.

Figure 5.3: Body force F is related to quantities on any contour Souter enclosing the body. Third dimension y and sideforce Y are not shown.

The viscous stress r ■ n was assumed to be negligible on Souter and has been left out of (5.13), although it could be retained if appropriate. As before, — p was replaced with p»—p in (5.13) with no effect. Also, V was replaced with V—V» which is allowed because of the mass conservation integral for the volume.

S P(V■ П) dS = 0 (5.14)

outer

The integral (5.13) gives an alternative way to calculate the force F on the body, using flow quantities on any surface Souter surrounding the body. Although it’s called the “far-field force." the integral is valid for any distance of the Souter contour, provided only that r ■ П on it is negligible as assumed. A distant placement is required only if far-field models are used to estimate the p and V needed to evaluate the integral.